|
Читайте также: |
В некоторых задачах ЕГЭ требуется найти синус, косинус или тангенс внешнего угла треугольника. А что такое внешний угол треугольника?
Давайте вспомним сначала, что такое смежные углы. Вот они, на рисунке. У смежных углов одна сторона общая, а две другие лежат на одной прямой. Сумма смежных углов равна 180°.
Возьмем треугольник и продолжим одну из его сторон. Внешний угол при вершине А — это угол, смежный с углом А. Если угол А острый, то смежный с ним угол — тупой, и наоборот.
Обратите внимание, что:
sin (180°-α) = sin α
cos (180°-α) = — cos α
tg (180°-α) = — tg α
Запомните эти важные соотношения. Сейчас мы берем их без доказательств. В разделе «Тригонометрия», в теме «Тригонометрический круг», мы вернемся к ним.
Легко доказать, что внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
1. В треугольнике ABC угол C равен 90°, 
. Найдите тангенс внешнего угла при вершине A.
Пусть 
— внешний угол при вершине А.
Зная cos , найдем tg по формуле
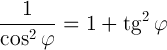
Получим: 
2. В треугольнике ABC угол C равен 90°, cos A = 0,1. Найдите синус внешнего угла при вершине B.
Задача решается за четыре секунды. Поскольку сумма углов А и В равна 90°, sin B = cos A = 0,1. Тогда и синус внешнего угла при вершине В также равен 0,1.
Дата добавления: 2015-08-17; просмотров: 566 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Тригонометрический круг: вся тригонометрия на одном рисунке | | | Высота в прямоугольном треугольнике |