Высота в прямоугольном треугольнике

Вспомним, что высота треугольника — это перпендикуляр, опущенный из его вершины на противоположную сторону.

В прямоугольном треугольнике катеты являются высотами друг к другу. Главный интерес представляет высота, проведённая к гипотенузе.

Один из типов экзаменационных задач В6 в банке заданий ФИПИ — такие, где в прямоугольном треугольнике высота проведена из вершины прямого угла. Посмотрим, что получается:

Высота проведена к гипотенузе АВ. Она делит треугольник АВС на два прямоугольных треугольника — АСН и СНВ. Смотрим внимательно на рисунок и находим на нем равные углы. Это и есть ключ к задачам по геометрии, в которых высота опущена на гипотенузу.

Мы помним, что сумма двух острых углов прямоугольного треугольника равна 90º. Значит, ∠ АСН = 90º — ∠ САН, то есть угол АСН равен углу АВС. Аналогично, угол САВ равен углу НСВ.

Иными словами, каждый из трех углов треугольника АВС равен одному из углов треугольника АСН (и треугольника ВСН). Треугольники АВС, АСН и ВСН называются подобными. Давайте нарисуем их рядом друг с другом.

Они отличаются только размерами. Стороны подобных треугольников пропорциональны. Что это значит?

Возьмем треугольники АСН и АВС. Стороны треугольника АВС длиннее, чем стороны треугольника АСН в k раз:

При решении задач нам пригодится равенство углов треугольников АВС, АСН и ВСН, а также пропорциональность их сторон. Обратите также внимание, что площадь треугольника АВС можно записать двумя разными способами: как половину произведения катетов и как половину произведения гипотенузы на проведенную к ней высоту.

1. В треугольнике ABC угол C равен 90°, CH — высота, ВС = 3, . Найдите AH.

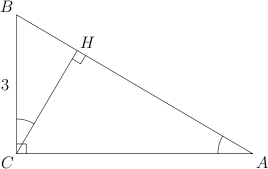
Рассмотрим треугольник АВС. В нем известны косинус угла А и противолежащий катет ВС. Зная синус угла А, мы могли бы найти гипотенузу АВ. Так давайте найдем sin A:

(поскольку значение синуса острого угла положительно). Тогда:

Рассмотрим прямоугольный треугольник ВСН, ∠ Н = 90°. Поскольку ∠ НСВ = ∠ А,

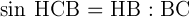
Отсюда

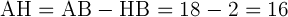
Ответ: 16.

2. В треугольнике ABC угол C равен 90º, АC = 8, sin A = 0,5. Найдите высоту CH.

Сделайте чертеж и рассмотрите прямоугольный треугольник АСН.

Ответ: 4.

3. В треугольнике ABC угол C равен 90º, АВ = 13, . К гипотенузе проведена высота CH. Найдите AH. <.

Это чуть более сложная задача. Ведь вам неизвестны катеты a и b.

Зато можно записать теорему Пифагора: a² + b² = 13².

Нам известно также, что:

Решая эту систему из двух уравнений, найдем:

;

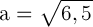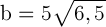
Запишем площадь треугольника АВС двумя способами:

и найдем СН = 2,5.

Дата добавления: 2015-08-17