
|
Читайте также: |
Высота треугольника
Определение 1. Высотой треугольника называют перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противолежащую сторону треугольника. Основанием высоты называют основание этого перпендикуляра (рис.1).
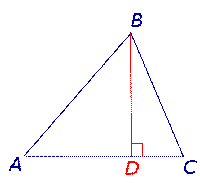
Рис.1
На рисунке 1 изображена высота BD, проведённая из вершины B треугольника ABC. Точка D – основание высоты.
Для высоты прямоугольного треугольника, проведённой из вершины прямого угла, справедливо следующее утверждение.
Утверждение. Длина высоты прямоугольного треугольника, опущенной на гипотенузу, являетсясредним геометрическим между длинами отрезков, на которые основание высоты делит гипотенузу (рис.2).

Рис.2
Доказательство. Углы треугольников BCD и ACD (рис.2) удовлетворяют соотношениям

В силу признака подобия прямоугольных треугольников треугольники BCD и ACD подобны. Следовательно,

Таким образом, длина отрезка CD является средним геометрическим между длинами отрезков BD и AD, что и требовалось доказать.
Высоты можно провести из каждой вершины треугольника, однако у треугольников различных типов высоты располагаются по-разному, как показано в следующей таблице.
Дата добавления: 2015-08-17; просмотров: 108 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ПРАВИЛА ПОВЕДЕНИЯ ПАССАЖИРОВ НА БОРТУ СУДНА. | | | Расположение высот у треугольников различных типов |