
Читайте также:
|
Это легко доказать. Нарисуйте треугольник. Через одну из его вершин проведите прямую, параллельную противоположной стороне, и найдите на рисунке равные углы. Сравните с решением в конце статьи.

А мы разберем задачи ЕГЭ, в которых фигурирует сумма углов треугольника.
1. Один из внешних углов треугольника равен 85º. Углы, не смежные с данным внешним углом, относятся как 2:3. Найдите наибольший из них. Ответ дайте в градусах.
Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним. Следовательно, сумма двух других углов треугольника равна 85°, а их отношение равно 2:3. Пусть эти углы равны 2х и 3х. Получим уравнение
2х + 3х = 85 и найдем х = 17.
Тогда 3х = 51.
Ответ: 51.
2. Один из углов равнобедренного треугольника равен 98º. Найдите один из других его углов. Ответ дайте в градусах.
Как вы думаете, может ли равнобедренный треугольник иметь два угла по 98°?
Нет, конечно! Ведь сумма углов треугольника равна 180°. Значит, один из углов треугольника равен 98°, а два других равны  .
.
Ответ: 41.
3. На рисунке угол 1 равен 46º, угол 2 равен 30º, угол 3 равен 44º. Найдите угол 4. Ответ дайте в градусах.
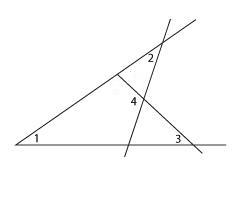
Давайте отметим на чертеже еще несколько углов. Они нам понадобятся.

Сначала найдем угол 5.
Он равен 180° - ∠1 - ∠3 = 90°
Тогда ∠6 = 90°
∠7 = 180° - ∠2 - ∠6 = 60°,
Угол 4, смежный с углом 7 равен 120°.
Ответ: 120.
Заметим, что такой способ решения — не единственный. Просто находите и отмечайте на чертеже все углы, которые можно найти.
4. Углы треугольника относятся как 2:3:4. Найдите меньший из них. Ответ дайте в градусах.
Пусть углы треугольника равны 2х, 3х и 4х. Запишем, чему равна сумма углов этого треугольника.
2х + 3х + 4х = 180°
9х = 180°
х = 20°
Тогда 2х = 40°.
Ответ: 40.
Дата добавления: 2015-08-17; просмотров: 327 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Высота в прямоугольном треугольнике | | | Углы при параллельных прямых и секущей. Вертикальные, смежные, односторонние, соответственные, накрест лежащие углы |