Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АрхитектураБиологияГеографияДругоеИностранные языки
ИнформатикаИсторияКультураЛитератураМатематика
МедицинаМеханикаОбразованиеОхрана трудаПедагогика
ПолитикаПравоПрограммированиеПсихологияРелигия
СоциологияСпортСтроительствоФизикаФилософия
ФинансыХимияЭкологияЭкономикаЭлектроника

Квадрат — определение и свойства

Синус, косинус и тангенс острого угла прямоугольного треугольника | Тригонометрический круг: вся тригонометрия на одном рисунке | Внешний угол треугольника. Синус и косинус внешнего угла | Высота в прямоугольном треугольнике | Сумма треугольника равна 180 градусов. | Углы при параллельных прямых и секущей. Вертикальные, смежные, односторонние, соответственные, накрест лежащие углы | Элементы треугольника. Высоты, медианы, биссектрисы | Четырехугольники. Сумма углов четырехугольника. Параллелограмм. Виды параллелограммов и их свойства. Ромб, прямоугольник, квадрат. Трапеция и ее свойства | Параллелограмм и его свойства. Площадь параллелограмма. Биссектрисы углов параллелограмма | Прямоугольник и его свойства |


Читайте также:
  1. Attribute – определение
  2. B)& Решение, определение, постановление и судебный приказ
  3. Defining and instantiating classes Определение и создание экземпляра классы
  4. Defining functions Определение функции
  5. Defining lazy properties Определение ленивых свойства
  6. III. Основные эксплуатационные свойства топлив
  7. Innate qualities – Свойства личности

Квадрат — это прямоугольник, у которого все стороны равны.
Можно дать и другое определение квадрата:
квадрат — это ромб, у которого все углы прямые.

Получается, что квадрат обладает всеми свойствами параллелограмма, прямоугольника и ромба.

Перечислим свойства квадрата:

  1. Все углы квадрата — прямые, все стороны квадрата — равны.
  2. Диагонали квадрата равны и пересекаются под прямым углом.
  3. Диагонали квадрата делят его углы пополам.

Площадь квадрата, очевидно, равна квадрату его стороны: S = a2.
Диагональ квадрата равна произведению его стороны на , то есть
,

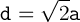Разберем несколько простых задач на тему «Квадрат». Все они взяты из Банка заданий ФИПИ.

1. Найдите сторону квадрата, диагональ которого равна .

Мы знаем, что 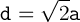. Тогда .

2. Найдите радиус окружности, описанной около квадрата со стороной, равной .

Очевидно, радиус окружности равен диагонали квадрата.

Ответ: 4.

3. Найдите сторону квадрата, описанного около окружности радиуса 4.

Диаметр окружности равен стороне квадрата.

Ответ: 8.

4. Найдите радиус окружности, вписанной в квадрат ABCD, считая стороны квадратных клеток равными .

Чуть более сложная задача. Нарисуйте окружность, вписанную в данный квадрат, то есть касающуюся всех его сторон. Вы увидите, что диаметр этой окружности равен стороне квадрата.

Ответ: 2.

5. Найдите радиус r окружности, вписанной в четырехугольник ABCD. В ответе укажите .

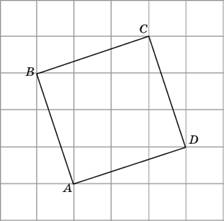
Считаем стороны клеток равными единице. Четырехугольник ABCD — квадрат. Все его стороны равны, все углы — прямые. Как и в предыдущей задаче, радиус окружности, вписанной в квадрат, равен половине его стороны.

Найдем на чертеже прямоугольный треугольник. По теореме Пифагора найдем сторону, например, АВ. Она равна . Тогда радиус вписанной окружности равен 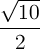. В ответ запишем .

Ответ: 5.

Дата добавления: 2015-08-17; просмотров: 85 | Нарушение авторских прав

<== предыдущая страница | следующая страница ==>
Ромб и его свойства| Трапеция и ее свойства
mybiblioteka.su - 2015-2024 год. (0.006 сек.)