Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АрхитектураБиологияГеографияДругоеИностранные языки
ИнформатикаИсторияКультураЛитератураМатематика
МедицинаМеханикаОбразованиеОхрана трудаПедагогика
ПолитикаПравоПрограммированиеПсихологияРелигия
СоциологияСпортСтроительствоФизикаФилософия
ФинансыХимияЭкологияЭкономикаЭлектроника

Ромб и его свойства

Геометрия на ЕГЭ по математике | Синус, косинус и тангенс острого угла прямоугольного треугольника | Тригонометрический круг: вся тригонометрия на одном рисунке | Внешний угол треугольника. Синус и косинус внешнего угла | Высота в прямоугольном треугольнике | Сумма треугольника равна 180 градусов. | Углы при параллельных прямых и секущей. Вертикальные, смежные, односторонние, соответственные, накрест лежащие углы | Элементы треугольника. Высоты, медианы, биссектрисы | Четырехугольники. Сумма углов четырехугольника. Параллелограмм. Виды параллелограммов и их свойства. Ромб, прямоугольник, квадрат. Трапеция и ее свойства | Параллелограмм и его свойства. Площадь параллелограмма. Биссектрисы углов параллелограмма |


Читайте также:
  1. Defining lazy properties Определение ленивых свойства
  2. III. Основные эксплуатационные свойства топлив
  3. Innate qualities – Свойства личности
  4. Using type properties and methods Используя свойства и методы типа
  5. VIII. Свойства природных каменных материалов.
  6. XXXVII. О СВОЙСТВАХ ТАТАР
  7. Абсорбционная осушка природного газа.Жидкие осушители и их свойства.

По определению, ромб — это параллелограмм, все стороны которого равны.

Свойства ромба:

  1. Диагонали ромба перпендикулярны.
  2. Диагонали ромба делят его углы пополам.

Воспользуемся свойствами ромба для решения задач.

1. Найдите меньшую диагональ ромба, стороны которого равны 2, а острый угол равен 60°.

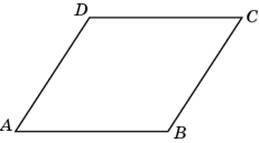
Проведите меньшую диагональ ромба и рассмотрите треугольник ADB. Поскольку AD = DB, а угол DAB равен 60°, треугольник ADB — равносторонний. Следовательно, меньшая диагональ ромба равна 2.

1. Найдите высоту ромба, сторона которого равна v3, а острый угол равен 60?.

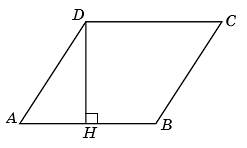
Один из подходов к решению задач по геометрии — метод площадей. Он состоит в том, что площадь фигуры выражается двумя разными способами, а затем из полученного уравнения находится неизвестная величина.

Пусть а — сторона ромба. Тогда

S = a2 sin 60° = ah,

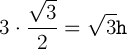
Отсюда .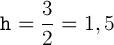

2. Диагонали ромба относятся как 3:4. Периметр ромба равен 200. Найдите высоту ромба.

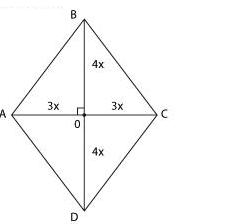
Пусть диагонали ромба равны 6х и 8х.
Диагонали ромба перпендикулярны, значит, треугольник АОВ — прямоугольный.
По теореме Пифагора АВ2 = АО2 + ОВ2
АВ2 = 9×2 + 16×2,
АВ2 = 25×2,
Отсюда АВ = 5х.
Поскольку периметр равен 200,
5х · 4 = 200
х = 10, АВ = 50, а диагонали ромба равны 60 и 80.

Нам надо найти высоту ромба.
Давайте запишем, чему равна площадь ромба. С одной стороны, S = ah. С другой стороны, площадь ромба складывается из площадей двух равных треугольников АВС и ADC, то есть равна 60 · 40 = 2400.
Отсюда h = S: a = 2400: 50 = 48.

Ответ: 48.

Дата добавления: 2015-08-17; просмотров: 171 | Нарушение авторских прав

<== предыдущая страница | следующая страница ==>
Прямоугольник и его свойства| Квадрат — определение и свойства
mybiblioteka.su - 2015-2024 год. (0.005 сек.)