Читайте также:
|
Параллелограмм — это четырехугольник, имеющий две пары параллельных сторон.
Свойства параллелограмма:
Давайте посмотрим, как свойства параллелограмма применяются в решении задач ЕГЭ.
1. Найдите угол между биссектрисами углов параллелограмма, прилежащих к одной стороне. Ответ дайте в градусах.
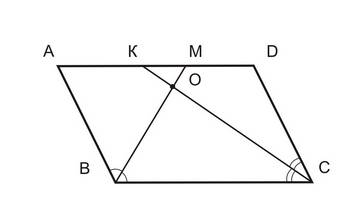
Пусть ВМ и СК — биссектрисы углов параллелограмма, прилежащих к стороне ВС. Сумма углов АВС и BCD равна 180°. Углы ОВС и ОСВ — половинки углов АВС и ВСD. Значит, сумма углов АВС и ВСD равна 90 градусов. Из треугольника ВОС находим, что угол ВОС — прямой.
Ответ: 90.
Биссектрисы углов параллелограмма, прилежащих к одной стороне, — перпендикулярны.
Легко доказывается и другое свойство биссектрис параллелограмма:
Биссектрисы противоположных углов параллелограмма — параллельны.
2. Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 5. Найдите его большую сторону.
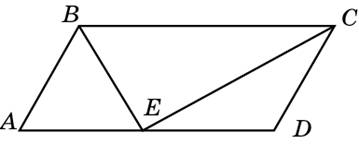
Найдем на этом рисунке накрест лежащие углы. Мы уже рассказывали, что это такое.
Углы СВЕ и ВЕА, а также СЕD и ВСЕ — накрест лежащие. Накрест лежащие углы равны. Значит, угол СВЕ равен углу ВЕА, а угол СЕD — углу ВСЕ.
Получаем, что треугольники АВС и CDE — равнобедренные, то есть АЕ = АВ, а DЕ = CD. Тогда AD = 5 + 5 = 10.
Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.
Запишем формулы площади параллелограмма:
S = ah, где а — основание параллелограмма, h — его высота.
S = ab sin φ, где а и b — стороны параллелограмма, φ — угол между ними.
И еще одна формула. Так же, как и свойства биссектрис углов параллелограмма, эта формула пригодится тем, кто нацелен на решение задачи С4.
S = 
d1 d2 sin α, где d1 и d2 — диагонали параллелограмма, α — угол между ними.
Дата добавления: 2015-08-17; просмотров: 397 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Четырехугольники. Сумма углов четырехугольника. Параллелограмм. Виды параллелограммов и их свойства. Ромб, прямоугольник, квадрат. Трапеция и ее свойства | | | Прямоугольник и его свойства |