Читайте также:
|
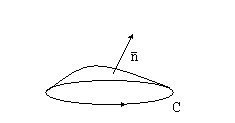
Пусть C – гладкая замкнутая пространственная кривая, S – такая двусторонняя поверхность, что кривая C является границей этой поверхности. Тогда справедлива формула Стокса
,
где выбор стороны поверхности, а значит, выбор знаков направляющих косинусов нормали к поверхности определяется заданием обхода по кривой C следующим образом: если глядеть с конца вектора нормали к поверхности C, должно быть видно, что обход кривой C совершается против часовой стрелки.
Следует пояснить, что собой представляет правая часть формулы Стокса. Под интегралом находится определитель, в верхней строке которого расположены направляющие косинусы вектора нормали к поверхности S, в средней строке расположены символические операторы нахождения частных производных, и в нижней строке расположены функции, представленные в криволинейном интеграле. Раскладывая определитель по верхней строке, мы получим поверхностный интеграл второго рода. Формальное «умножение» символического оператора на функцию означает, что от этой функции следует взять частную производную по соответствующей переменной.
В частном случае – когда поверхность S – это плоскость XOY, то есть 
, формула Стокса превращается в формулу Грина.
Дата добавления: 2015-08-17; просмотров: 59 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Поверхностный интеграл второго рода. | | | Связь интеграла по замкнутой поверхности с тройным интегралом по телу, ограниченному этой поверхностью. Формула Гаусса-Остроградского. |