Теорема Лапласа

Обобщим понятие алгебраического дополнения.

Определение 1. Дополнительным минором будем называть определитель (n – p)-порядка, полученный вычёркиванием p соответствующих строк и столбцов.

Определение 2. Алгебраическим дополнением минора 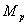будем называть произведение дополнительного минора на

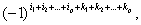
т.е.

, (5)

где

сумма номеров строк и столбцов минора .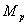

Для примера рассмотрим определитель четвёртого порядка:

Выберем

тогда дополнительным минором будет

далее запишем по формуле (5):

Теорема Лапласа

Пусть в определителе порядка n выбраны нами k строк. Тогда сумма произведений миноров k -го порядка, содержащихся в указанных строках, на соответствующие алгебраические дополнения равна этому определителю.

Теорему проиллюстрируем на примере определителя четвёртого порядка. Выберем первую и третью строки, из них составим миноры и умножим их на соответствующие алгебраические дополнения:

Теорема Лапласа позволяет сводить вычисление определителя n -го порядка к вычислению нескольких определителей порядка k < n. Этих новых определителей оказывается довольно много и поэтому теорему Лапласа применять целесообразно лишь в том случае, когда в определителе можно так выбрать k строк, что многие из миноров k -го порядка, расположенных в этих строках, будут равны нулю.

Дата добавления: 2015-08-17