
Читайте также:
|
Определители
Понятие определителя n-го порядка и общий алгоритм решения определителя
Свойства определителя n-го порядка
Миноры и алгебраические дополнения
Теорема Лапласа
Понятие определителя n-го порядка
Часто говорят также "определитель матрицы", поэтому сначала объясним, что такое матрица. Матрица - это прямоугольная таблица, составленная из чисел, которые нельзя менять местами. Квадратная матрица - таблица, у которой число строк и число столбцов одинаково. Определитель может быть только у квадратной матрицы.
Итак, пусть дана квадратная таблица, состоящая из чисел, расположенных в n строках (горизонтальных рядах) и в n столбцах (вертикальных рядах). С помощью этих чисел по некоторым правилам, которые мы изучим ниже, находят число, которое и называют определителем n -го порядка и обозначают следующим образом:
 (1)
(1)
Числа  называют элементами определителя (1) (первый индекс означает номер строки, второй – номер столбца, на пересечении которых стоит элемент; i = 1, 2,..., n; j = 1, 2,..., n). Порядок определителя – это число его строк и столбцов.
называют элементами определителя (1) (первый индекс означает номер строки, второй – номер столбца, на пересечении которых стоит элемент; i = 1, 2,..., n; j = 1, 2,..., n). Порядок определителя – это число его строк и столбцов.
Чтобы читателю был более понятен практический смысл составления матриц и определителей, упомянём один из многочисленных примеров. Если три магазина одной сети продают три различных вида товаров, то отчёт о продажах за год можно представить в виде таблицы из трёх строк и трёх столбцов, содержащей некоторые числа. Первый индекс каждого числа - это номер магазина, а второй - номер вида товара.
Определители играют важную роль в решении систем линейных уравнений. А один из примеров, когда надо решить систему уравннений - вычисление величины факторов, влияющих на Ваше настроение. Здесь система линейных уравнений решается для получения коэффициентов линейной множественной регрессии, которые и являются измерением влияния.
Но мы уже забежали вперёд, а пока нам надо научиться решать определители.
Ниже приведём общий алгоритм нахождения определителей, а затем последует разбор действий, в нём перечисленных:
Теперь каждое из действий алгоритма подробно разберём - технологически и на примерах.
Воображаемая прямая, соединяющая элементы определителя, у которых оба индекса одинаковы, т.е. элементы

называется главной диагональю, другая диагональ – побочной.
Покажем, как вычисляются определители первых трёх порядков.
Определитель первого порядка – это сам элемент  т.е.
т.е.
 .
.
Определитель второго порядка есть число, получаемое следующим образом:
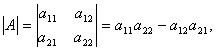 (2)
(2)
где
 и
и 
- произведение элементов, стоящих соответственно на главной и на побочной диагоналях.
Равенство (2) показывает, что со своим знаком берётся произведение элементов главной диагонали, а с противоположным – произведение элементов побочной диагонали.
Пример 1. Вычислить определители второго порядка:


Решение. По формуле (2) находим:


Определитель третьего порядка – это число, получаемое так:
 (3)
(3)
Запомнить эту формулу трудно. Однако существует простое правило, называемое правилом треугольников, которое позволяет легко воспроизвести выражение (3). Обозначая элементы определителя точками, соединим отрезками прямой те из них, которые дают произведения элементов определителя (рис. 1).

Формула (3) показывает, что со своими знаками берутся произведения элементов главной диагонали, а также элементов, расположенных в вершинах двух треугольников, основания которых ей параллельны; с противоположными – произведения элементов побочной диагонали, а также элементов, расположенных в вершинах двух треугольников, которые ей параллельны.
На рис.1 главная диагональ и соответствующие ей основания треугольников и побочная диагональ и соответствующие ей основания треугольников выделены красным цветом.
При вычислении определителей очень важно, как и в средней школе, помнить, что число со знаком минус, умноженное на число со знаком минус, в результате даёт число со знаком плюс, а число со знаком плюс, умноженное на число со знаком минус, в результате даёт число со знаком минус.
Пример 2. Вычислить определитель третьего порядка:

Решение. Пользуясь правилом треугольников, получим


Вычисление определителей четвертого и последующих порядков можно свести к вычислению определителей второго и третьего порядков. Это можно сделать с помощью свойств определителей. К рассмотрению их мы и переходим.
Дата добавления: 2015-08-17; просмотров: 137 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Типы семейных структур | | | Свойства определителя n-го порядка |