Етод максимального правдоподобия

Оценкой максимального правдоподобия неизвестного параметра по группированным наблюдениям называется такое значение параметра, при котором функция правдоподобия

, (1.2.1)

где - некоторая константа и - вероятность попадания на­­блю­дения в -ый интервал значений, достигает максимума на множестве возможных зна­чений параметра. Здесь предполагается, что для всех . Для вычисления ОМП дифференцируют функ­цию правдоподобия по и, приравнивая производные нулю, получают систему уравнений правдоподобия

,

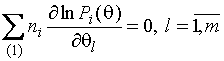где 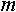- размерность вектора параметров .

Функция правдоподобия для частично группированной выборки имеет вид

,

система уравнений правдоподобия

,

где 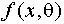- функция плотности случайной величины, (1) и (2) означают, что суммирование и умножение осуществляются по интервалам с группированными и негруппированными данными соответственно.

В случае достаточно больших 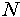при определенных условиях регулярности для функции плотности ОМП существует практически всегда, состоятельна и асимптотически эффективна. Условия существования, асимптотической эффек­тив­ности и состоятельности по группированным и цензурированным выборкам рассматривались в работах Г. Куллдорфа и Н.А. Бодина. Г.Г. Зачепой были получены условия существования ОМП основных параметров распределения Вейбулла и гамма-рас­пре­де­ления. В наших работах получены условия сущест­вования и единственности ОМП для параметров ряда непрерывных законов распределения случайных величин.

Вообще говоря, метод максимального правдоподобия требует значительного объема вычислений. А в случае группированных или частично группированных данных возникает необходимость в решении задач численного интегрирования, в том числе, и вычисления несобственных интегралов. Именно трудности вычисли­тельного характера, особенно в ситуации группированных и частично группиро­ванных данных, ограничивали использование метода максимального правдоподобия.

Существует большое число работ, в которых рассматривается вычисление приближенных оценок максимального правдоподобия. В этом случае исходная группированная выборка заменяется негруппированной, в которой индивидуальным значениям присваиваются значения центров интервалов группирования при их равной длине. Далее вычисляются оценки, а затем выводятся выражения для поправок к полученным оценкам.

Описанные в данном разделе методы вычисления оценок параметров распределений далеко не представляют собой полный перечень всех возможных методов, да эта цель и не преследовалась.

33.Методнаименьшихквадратов.

Метод наименьших квадратов (МНК, OLS, Ordinary Least Squares) — один из базовых методоврегрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным. Метод основан на минимизации суммы квадратов остатков регрессии.

Необходимо отметить, что собственно методом наименьших квадратов можно назвать метод решения задачи в любой области, если решение заключается или удовлетворяет некоторому критерию минимизации суммы квадратов некоторых функций от искомых переменных. Поэтому метод наименьших квадратов может применяться также для приближённого представления (аппроксимации) заданной функции другими (более простыми) функциями, при нахождении совокупности величин, удовлетворяющих уравнениям или ограничениям, количество которых превышает количество этих величин и т.д.

Дата добавления: 2015-08-17