Теорема о базисном миноре матрицы

Определители | Примеры. | Свойства операции транспонирования матриц. |

Читайте также:

Алгоритм не должен изменяться при изменении размеров матрицы.
В двумерном массиве первый индекс – строка, второй – столбец. В трёхмерном - строка, столбец, номер матрицы и т. д.
В настоящее время имеется готовые матрицы на двух языках. Немецкий, Английский(Британский). Вы их можете приобрести на моем сайте
Векторы и матрицы
Вписанные и описанные треугольники. Еще две формулы площади треугольника. Теорема синусов
Две точки между 2 и 5 набираются нажатием клавиши с русской буквой Ж клавиатуры на латинской раскладке или кнопки m.. n панели матрицы.
Интегральная сумма, определенный интеграл (определение, теорема существования, основные свойства, правила вычисления)

1°. Линейная зависимость строк матрицы.

Определение 1. Строки 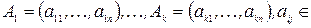R назовем линейно зависимыми, если такие 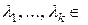R, одновременно не равные нулю, такие что

Строки, не являющиеся линейно зависимыми, являются линейно независимыми. Иными словами, 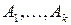– линейно независимы, если равенство возможно лишь когда .

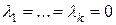Теорема 1. Строки 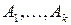– линейно зависимы 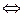одна из этих строк является линейной комбинацией остальных.

Дата добавления: 2015-08-17; просмотров: 35 | Нарушение авторских прав

<== предыдущая страница	\|	следующая страница ==>
Доказательство.	\|	Доказательство.

mybiblioteka.su - 2015-2024 год. (0.006 сек.)