Примеры.

1. .

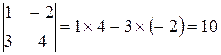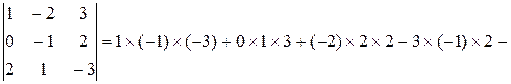
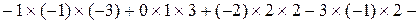
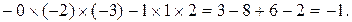
3.

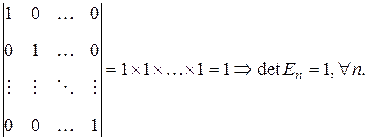
4.

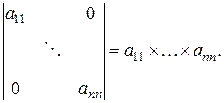
5.

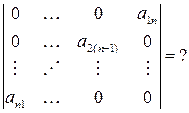
6.

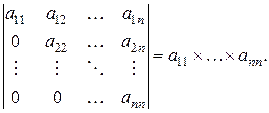
7.

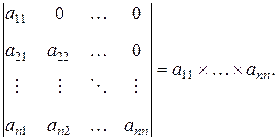
Для определителей порядка большего 3 нет единых правил вычисления и, как правило, такие определители вычисляют с использованием свойств определителя.

2⁰. Транспонирование матриц. Определитель транспонированной матрицы.

Пусть 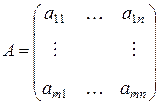Î R .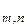

Определение 2. Матрица 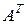= 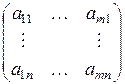Î R 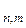называется транспонированной к матрице 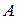, если она получается следующим образом: 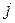–й столбец матрицы 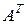состоит из элементов 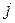–ой строки матрицы 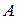, расположенных в том же порядке.

Операция 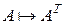называется транспонированием.

Пример. .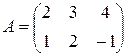

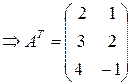Дата добавления: 2015-08-17