Определители

1⁰. Определение.

Определение 1. Определителем квадратной матрицы порядка 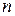с действительными элементами называется действительное число, обозначаемое:

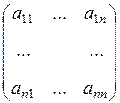или или ,

и равное

,

где сумма берется по всем перестановкам множества из 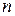элементов, – знак перестановки.

Таким образом, из элементов 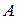составляются всевозможные произведения из 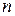сомножителей, содержащих по одному элементу из каждого столбца и каждой строки. Всего слагаемых в сумме равно числу перестановок, т.е. равно .

Замечание. Определитель бывает только у квадратных матриц.

Иногда вместо термина определитель используют термин детерминант (по латыни).

Примеры.

1. Если 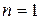, то матрица 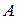состоит из одного элемента, т.е. . Тогда .

2. Если , то 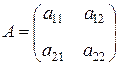. Формула для определителя в этом случае содержит слагаемых, соответствующих тождественной перестановке 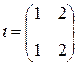, , 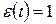и перестановке 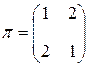, . Получаем

.

3. Если , то . В этом формула для определителя содержит 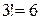слагаемых, соответствующих перестановкам

, , , ,

, , , ,

, , , .

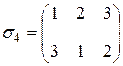Получаем

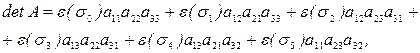
т.е.,

.

Слагаемые с положительными и отрицательными коэффициентами запоминаются по правилу Саррюса; а именно,

.

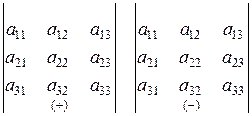Дата добавления: 2015-08-17