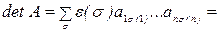
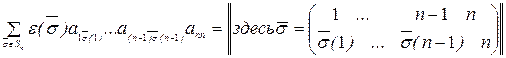
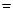
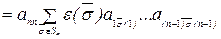Доказательство. Рассмотрим 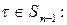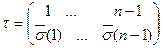. Очевидно, что 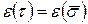, так что число инверсий в 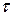и одно и тож

.

Рассмотрим . Очевидно, что , так что число инверсий в и 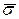одно и тоже; значит,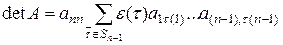 , что и требовалось доказать.

Вернемся к доказательству теоремы: 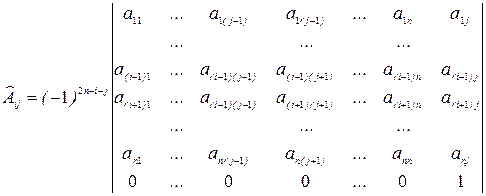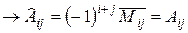, что и требовалось доказать.

Следствие (разложение по «чужой» строке).

Сумма произведений всех элементов какой–нибудь строки матрицы на алгебраические дополнения соответствующих элементов другой строки равна нулю.

Доказательство. Пусть 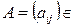R 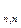. Рассмотрим матрицу 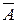, получающуюся из 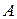заменой 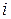–ой строки на 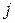–ю, оставляя 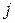–ю прежней 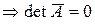. Напишем разложение 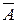по 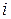–ой строке: 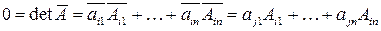, т.к. алгебраические дополнения к элементам 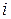–ой строки у матрицы и совпадают.

Пример:

1) =

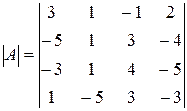
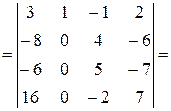
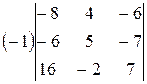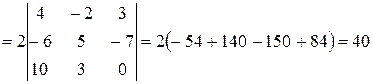
Следующая теорема обобщает теорему 1.

Теорема 2 (теорема Лапласа).

Пусть матрице 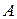порядка 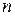произвольно выбраны 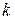строк, 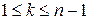. Тогда сумма произведений всех миноров 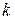–го порядка, содержащихся в выбранных строках, на их алгебраические дополнения, равна 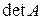. Т.е. если 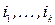– выбранные строки, то

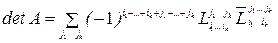(2),

где суммирование ведется по всевозможным значениям индексов 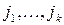таким, что .

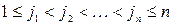Формула (2) называется формулой разложения определителя по 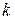строкам .

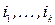Доказательство см.,например в книге Ильин В. А., Поздняк Э. Г. Линейная алгебра. М.: Наука, Физматлит, 1999. -296с. (стр. 25)

Примеры:

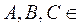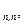
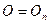1) Пусть R R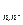

Тогда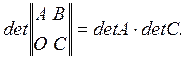

Доказательство в силу Теоремы 2 разложением по первым n строкам в силу .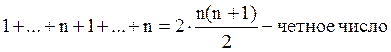

2)

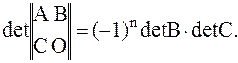
Доказательство в силу Теоремы 2 разложением по последним n строкам с учетом равенства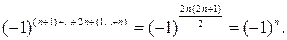

3) Определитель Вандермонда.

.

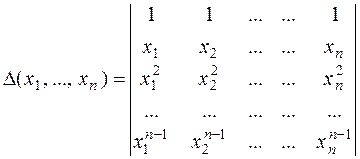Вычитая первый столбец из всех остальных, получаем:

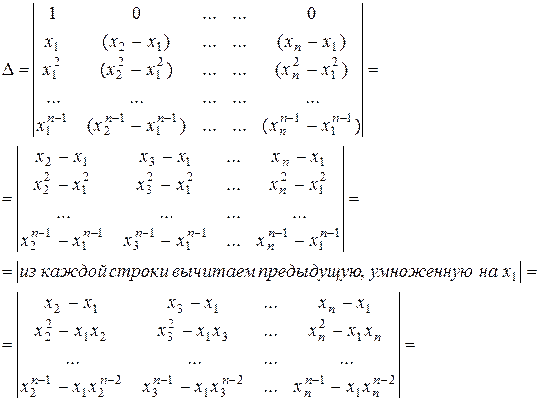
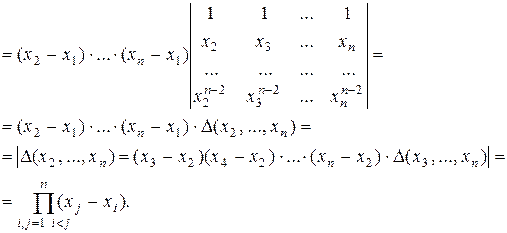
4°. Определитель суммы и произведения матриц.

Непосредственно из линейных свойств определителя вытекает:

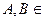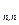Теорема 3. Если R , то 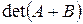равен сумме определителей матриц порядка 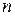, каждая из которой получается следующим образом: часть строк (столбцов) берутся совпадающими с соответствующими строками (столбцами) матрицы 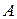, а остальные – совпадающие с соответствующими строками (столбцами) матрицы B.

Иллюстрация 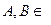R .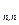

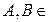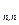Теорема 4. Если R , то .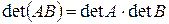

Доказательство. Рассмотрим матрицу 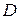порядка 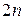: , где 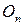– нулевая квадратная матрица порядка ,

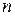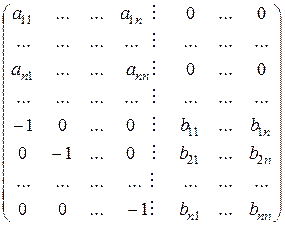
Из примера 1 пункта 3 имеем, что .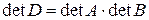

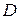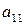Преобразуем теперь матрицу . строку умножим на , – на 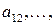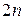–ую – на 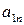и сложим с первой строкой. Тогда первая строка имеет вид: 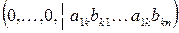. Аналогично к 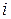–ой строке прибавим 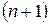, умноженную на 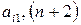– на 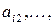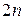–ую на .

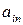Имеем: 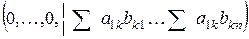. Т.о., первые 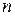строк принимают вид:

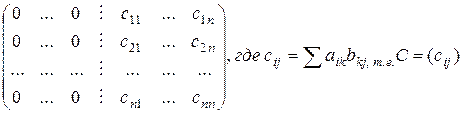
При таких преобразованиях определитель не меняется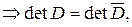

где 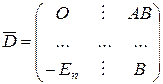. Но 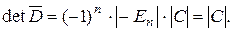Т.о., доказано, что

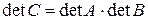det.

Следствие 1. Если 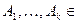R _n,n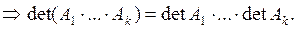

Следствие 2. Из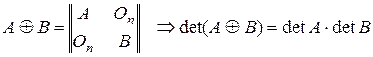

5°. Обратная матрица. Пусть 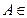R 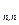– квадратная матрица порядка .

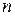Определение 7. Матрица 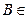R 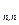называется обратной для 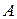, если

.

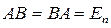Определение 8. Квадратная матрица 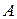называется невырожденной (или неособой), если 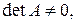и вырожденной (особой), если .

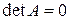Из теоремы 2 пункта 4 Þ произведение матриц, одна из которых вырождена, будет вырожденной матрицей, а произведение двух невырожденных матриц дает невырожденную матрицу.

Определение 9. Матрицей, присоединенной к матрице 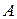, называется матрица

,

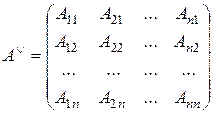где 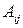– алгебраическое дополнение элемента 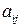матрицы .

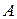Лемма. Для матриц 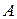и 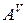справедливо .

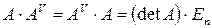Доказательство. Пусть 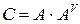. Тогда

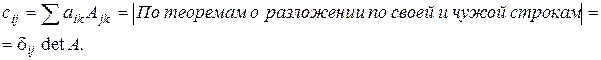
Итак, 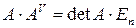. Аналогично .

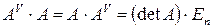Теорема 5. Для того, чтобы для матрицы 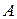существовала обратная, необходимо и достаточно, чтобы матрица 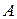была невырожденной.

Доказательство. Пусть для матрицы

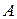
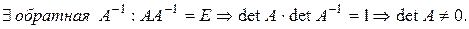
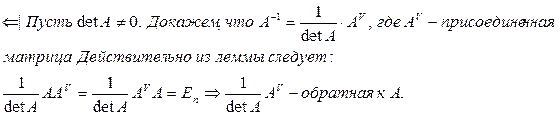
Замечание: итак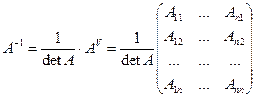

Пример:

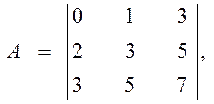
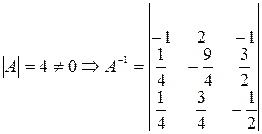
Свойства обратных матриц:

Пусть 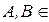R ^.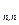

Тогда

1.

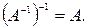
2.

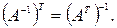
3.

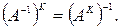
4.

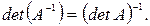
5.

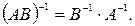
Дата добавления: 2015-08-17