
|
Читайте также: |
Если для группы из m товаров известны цена каждого товара рi и его товарооборот пi то средняя цена вычисляется по следующейформуле:
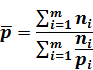
Отклонение цены товара Δ от средней цены равно 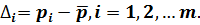
Удельный вес различных товаров в товарообороте ρi равен
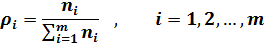
| Товар | Цена, руб. | Товарооборот, руб. |
| А | ||
| В |
Пример 20. Известны следующие данные.
Определим среднюю цену, отклонение цены каждого товара от средней цены и удельный вес различных товаров в товарообороте.
Здесь т = 2. Заполним таблицу.
| Товар | Pi | ni | 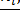
| 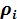
| 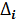
|
| А | 0,4 | -6,02 | |||
| В | 0,6 | 4,98 | |||
| Сумма | — | — |
Поясним, как заполняется таблица. Числа 2-го и 3-го столбцов взяты из исходной таблицы. Числа 3-го столбца делим на числа 2-го столбца, результат округляем до целого числа и пишем в 4-м столбце. В последней строке указана сумма чисел соответствующего столбца. Каждое число 3-го столбца делим на итоговую сумму чисел этого столбца и результат пишем в 5-м столбце. Там указан удельный вес различных товаров в товарообороте.
Средняя цена 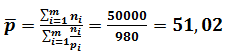 руб
руб
Из каждого числа 2-го столбца вычитаем среднюю цену
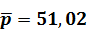 руб. и результат пишем в 6-м столбце. Там указаны отклонения цен товаров от средней цены.
руб. и результат пишем в 6-м столбце. Там указаны отклонения цен товаров от средней цены.
Задача 20. Известны следующие данные.
| Товар | Цена, руб. | Товарооборот, руб. |
| А | ||
| В |
Определить среднюю цену, отклонение цены каждого товара от средней цены и удельный вес различных товаров в товарообороте.
Среднюю цену по группе товара (мяса разных сортов и т.п.) можно рассчитать, зная относительные показатели структуры продаж, если известна цена товара рi и структура товарооборота di (%): 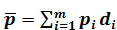 ,
,
где 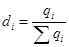 - удельный вес продажи каждого вида товара в общем объеме продаж.
- удельный вес продажи каждого вида товара в общем объеме продаж.
Пример 21. Известны следующие данные о цене и структуре товарооборота товара по группе А.
| Цена, руб. | Структура товарооборота, % |
| 0,3 | |
| 0,7 |
Определим среднюю цену товара А.
Средняя цена товара А равна 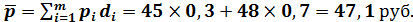
Задача 21. Известны следующие данные о цене и структуре товарооборота товара А.
| Цена, руб. | Структура товарооборота, % |
| 0,4 | |
| 0,6 |
Определить среднюю цену товара А.
Если известны, цена pi и объем продаж qi(в единицах), то средняя цена вычисляется по следующей формуле:
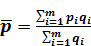
Размах вариации цен R — это разность между наибольшей ртах и наименьшей рmin ценами: R = pmax - pmin.
Cреднее квадратическое отклонение цен вычисляется по следующей формуле: 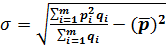 .
.
Коэффициент вариации цен вычисляется по следующей формуле: 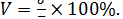
Пример 22. Известны следующие данные.
| Цена товара, руб. | Объем продаж, единиц |
Определим среднюю цену, размах вариации цен, среднее квадратическое отклонение цен и коэффициент вариации цен.
Здесь т = 3. Заполним таблицу.
| Номер | pi | qi | pi qi | 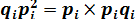 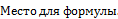 Q,p! = PiXPi 4, Q,p! = PiXPi 4,
|
| Сумма | — |
Числа 2-го и 3-го столбцов взяты из исходной таблицы. 4-й (5-й) столбец равен произведению 2- го и 3-го (4-го) столбцов. В последней строке указана сумма чисел соответствующего столбца.
Средняя цена 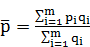 =
= 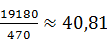 руб.
руб.
Размах вариации цен R = рmax — рmin = 44 — 38 = 6 руб.
Среднее квадратическое отклонение цен:
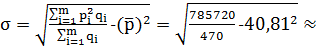 2,51 руб.
2,51 руб.
Коэффициент вариации цен 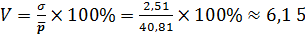 %.
%.
Задача 22. Известны следующие данные:
| Цена товара, руб. | Объем продаж, единиц |
Определить среднюю цену, размах вариации цен, среднее квадратическое отклонение цен и коэффициент вариации цен.
8 ОПРЕДЕЛЕНИЕ ЦЕНЫ МЕТОДОМ БАЛЛЬНЫХ ОЦЕНОК
Метод балльных оценок позволяет установить отпускные цены на новые модели.
Составляется список факторов, влияющих на отпускные цены товара. Для определения относительной значимости этих факторов каждому фактору приписывается вес — число из отрезка [0, 1]. Сумма всех весов должна равняться единице.
Выбирается шкала для измерения каждого фактора (например, от I до 10 или от 1 до 100 баллов). Для каждой новой модели нужно оценить все факторы по принятой шкале измерения. Суммарное число баллов по всем моделям для каждого фактора должно равняться выбранному максимуму (например, 10 или 100 баллов).
Умножим оценки факторов на соответствующие веса и суммируем полученные числа для каждой новой модели. Затем найдем среднюю экспертную оценку — среднее арифметическое итоговых сумм.
Зная среднюю рыночную цену товара, определим среднюю рыночную цену одного балла по следующей формуле:
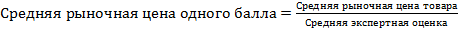
На основании средней рыночной цены одного балла определяется отпускная цена модели:
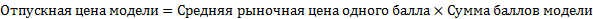
| Фактор | Вес | А | В |
| Удобство пользования | 0,5 | ||
| Дизайн | 0,3 | ||
| Упаковка | 0,2 |
Пример 23. Средняя рыночная цена товара равна 50 руб. Все данные отражены в таблице.
Определим отпускные цены на модели А и В методом балльных оценок.
Заполним таблицу.
| Фактор | Вес | А | В | Вес × А | Вес× В |
| Удобство пользования | 0,5 | ||||
| Дизайн | 0,3 | 1,5 | 1,5 | ||
| Упаковка | 0,2 | 0,6 | 1,4 | ||
| Сумма | 5,1 | 4,9 |
Поясним, как заполняется таблица. Числа 2-го столбца умножаем на числа 3-го (4-го) столбца соответственно и результат пишем в 5-м (6-м) столбце. В последней строке указана сумма чисел соответствующего столбца.
Средняя экспертная оценка равна (5,1 + 4,9)/2 = 5.
Тогда средняя рыночная цена одного балла = (средняя рыночная цена товара)/(средняя экспертная оценка) = 50/5 = 10.
Отсюда отпускная цена модели А —5,1×10 = 51 руб., а отпускная цена модели В — 4,9×10 = 49 руб.
Задача 23. Средняя рыночная цена товара равна 60 руб. Все данные отражены в таблице.
| Фактор | Вес | А | В |
| Удобство пользования | 0,45 | ||
| Дизайн | 0,35 | ||
| Упаковка | 0,2 |
Определить отпускные цены на модели А и В методом балльных оценок.
Дата добавления: 2015-08-17; просмотров: 92 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ЦЕНООБРАЗОВАНИЕ И МАРКЕТИНГ-МИКС | | | ОЦЕНКА ПОСТАВЩИКОВ |