Расчет сечений стальных пролетных строений

В проекте рекомендуется расчет конструкций металлических мостов выполнять в следующем порядке:

-расчет железобетонной или металлической плитыпроезжей части (в автодорожных и городских мостах);

-расчет продольных и поперечных балок или ребер ортотропной плиты с прикреплениями;

-расчет главных балок, ферм или арок с подбором сечений или элементов ферм, расчет стыков главной балки, арки или узлов ферм;

-расчет продольных и поперечных связей между главными балками или фермами и опорных частей, а также других элементов по указанию руководителя.

Сечения необходимо рассчитывать в такой последовательности:

-конструирование сечения;

-расчет геометрических характеристик с учетом стадийности работы элемента;

-расчет прочности, общей устойчивости и выносливости;

-проверка прикреплений (сварных швов или количества и шага высокопрочных болтов);

-определение мест изменения сечений и построение эпюры материалов;

-расчет на местную устойчивость стенки;

-расчет монтажных стыков или узлов фермы;

-определение прогибов и стрелы кривой строительного подъема.

В соответствии с [1] расчет стальных мостов должен выполнятся с учетом возможности развития ограниченных пластических деформаций.

При расчете прочности стальных изгибаемых элементов с учетом развития ограниченных пластических деформаций геометрические характеристики сечения необходимо вычислить не по фактическим геометрическим размерам, а с учетом эффективной ширины пояса b_ef. Для ее определения следует учитывать неравномерность распределения нормальных напряжений по ширине сечения и в соответствии с [ 1 ] знать отношение σ _min /σ _max. Здесь σ _min и σ _max – соответственно минимальное и максимальное напряжения на рассматриваемом участке главной балки, определяемые на основе пространственного расчета конструкции в упругой стадии. При отсутствии пространственных расчетов приближенно эффективную ширину поясов можно определить по рекомендациям, изложенным в [ 2 ] или использовать формулы, приложения к Eurocod [ 3 ].

Согласно рекомендациям Eurocod, эффективную ширину b_ef следует определять по формуле (3.1) в зависимости от формы эпюры моментов (рис.3.1).

b_ef = ∑ ν _i∙b_i, (3.1)

где ν _i и b_i – соответственно редукционный коэффициент и ширина пластинчатого элемента пояса.

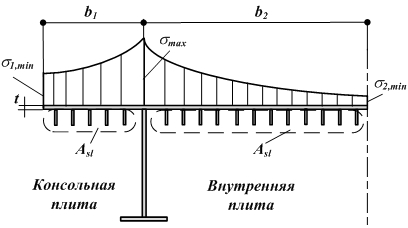
Рис.3.1.Схема определения коэффициента редукции для упругой работы

Редукционный коэффициент ν может быть определен по формулам таблицы 3.1 и параметру:

где A_sl – площадь продольных ребер плиты, t – толщина настила, L_e - эффективная длина пролета.

Таблица 3.1

Формулы для определения значений редукционного коэффициента

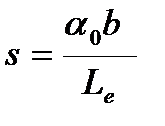
	Рассматриваемый участок	Значение коэффициента ν
≤ 0,02		ν= 1
0,02 – 0,70	Вогнутая эпюра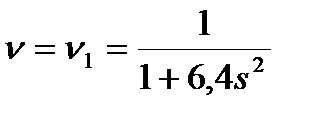
Выпуклая эпюра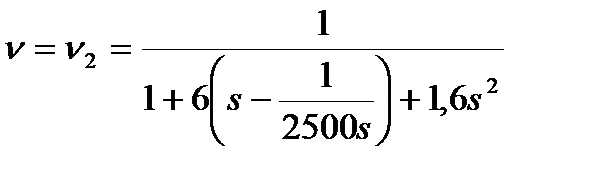
>0,70	Вогнутая эпюра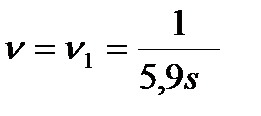
Выпуклая эпюра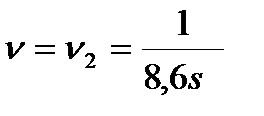
Все значения s	Конечное опирание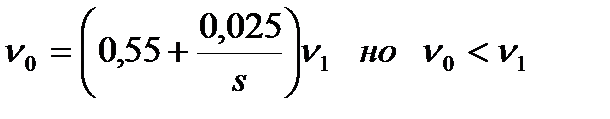
Все значения s	Консоль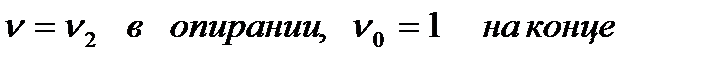

Эффективную длину пояса L_e для неразрезных балок можно определить, пользуясь схемой, изображенной на рис. 3.2, при условии, что нет пролетов длиннее 1,5 длины примыкающего пролета, а консоль не длиннее половины примыкающего пролета. В иных случаях длина пролета должна быть определена между нулевыми точками эпюры моментов. Для разрезных балок длина пояса равна длине пролета.

Расчет на прочность стальных изгибаемых элементов по нормальным напряжениям производят по формулам табл. 3.2.

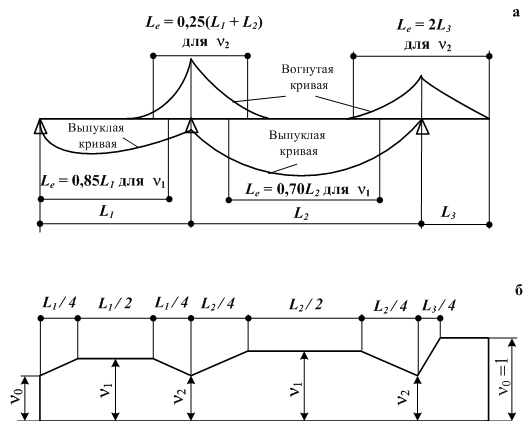
Рис.3.2. Схема к определению эффективной длины пролета

Таблица 3.2

Формулы для расчета на прочность по нормальным напряжениям

№ формул СП	Формулы	Пояснения
Проверка прочности по формуле 8.5
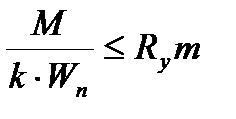
8.5[1].		Проверка прочности элементов, изгибаемых в одной из главных плоскостей. Ry – расчетное сопротивление стали (табл.8.5 [1]); m – коэффициент условий работы(табл.8.15 [1]); Wn – момент сопротивления сечения нетто, определяемый с учетом эффективной ширины пояса.
Вычисление коэффициента k Коэффициент k учитывает увеличение несущей способности сечения за счет развития ограниченных пластических деформаций, равных 0,06%
8.6[1].	k =k1	если τ m ≤ 0,25 Rs	При одновременном действии в сечении элемента момента M и поперечной силы Q. Rs =0,58 Ry – расчетное сопротивление стали на сдвиг.
8.7[1].	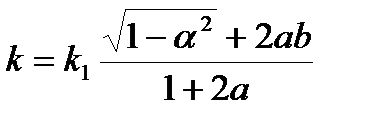при этом 0 ≤k ≤k1	если   0,25 Rs <τ m ≤ 0,25 Rs

Продолжение табл. 3.2

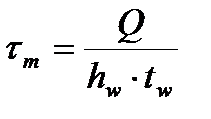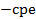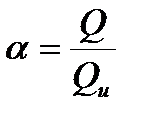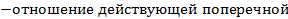Для кольцевых сечений k1 = 1,15.   Для прямоугольных и Н-образных сечений k1 = 1,25.   Для двутавровых, тавровых и коробчатых сечений коэффициент k1 определяется по табл. 8.16[1].	днее касательное напряжение в стенке;   к предельной;
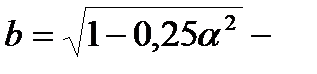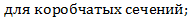
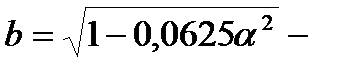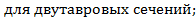
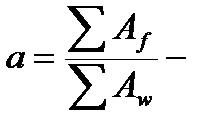
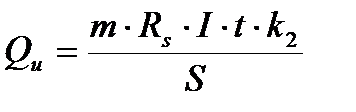
	Qu - предельная поперечная сила; 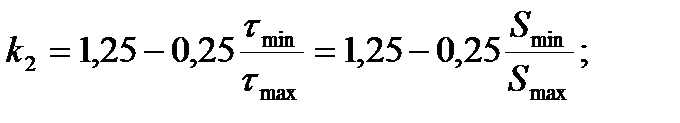  τmin и τmax – наименьшее и наибольшее значение напряжений в стенке при упругой работе; Smin и Smax –минимальное (для пояса) и максимальное (для полусечения) значение статического момента.

Кроме выполнения проверок прочности с учетом развития ограниченных пластических деформаций, следует ограничить величины напряжений, по формулам, приведенным в табл.3.3.

Из-за опасности хрупкого разрушения при высоких уровнях напряжений в растянутых элементах развитие пластических деформаций не допускается и условие прочности имеет вид (п.8.25 [ 1]):

где N – расчетная растягивающая сила; A_n –площадь поперечного сечения с учетом ослаблений.

Сжатые элементы рассчитываются на устойчивость. При центральном сжатии и сжатии с изгибом в плоскости наибольшей гибкости или соответствующем внецентренном сжатии расчет производится по формуле:

Таблица 3.3

Формулы для расчета напряжений в стенках балок

№ формул СП	Формулы	Пояснения
Ограничение касательных напряжений в стенках балок
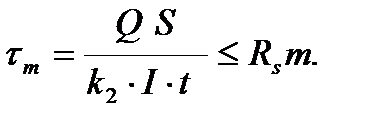
8.26		Проверка прочности по касательным напряжениям М = 0. При этом расчетное сопротивление стали на сдвиг Rs =0,58 Ry.
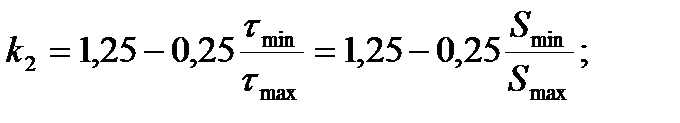
8.27		τmin и τmax – наименьшее и наибольшее значение напряжений в стенке при упругой работе; Smin и Smax – минимальное (для пояса) и максимальное (для полусечения) значение статического момента.
Ограничение приведенных напряжений в стенках балок
8.29	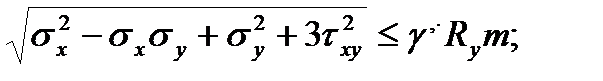τxy ≤ Rsm.	Проверка прочности по приведенным напряжениям. При этом γ’ = 1,15 при σ x = 0; γ’ = 1,1 при σ y ≠ 0;

В формуле (3.5) приняты обозначения: А – площадь сечения брутто; φ - коэффициент понижения несущей способности при проверке устойчивости центрально и внецентренно сжатых элементов, принимаемый по табл. Ф1-Ф3 [ 1 ] в зависимости от класса прочности стали, гибкости λ и приведенного относительного эксцентриситета в плоскости изгиба e_ef.

e_ef = η e_rel, (3.6)

где η – коэффициент влияния формы сечения, принимаемый по СП 16.13330;

e_rel = е /ρ – относительный эксцентриситет; е = M / N –расчетный эксцентриситет в плоскости изгиба, определяемый по наибольшему изгибающему моменту в пределах средней трети сжатого стержня; ρ = W_c / A –ядровое расстояние по направлению эксцентриситета е; W_c – момент сопротивления, вычисляемый для наиболее сжатого волокна.

Гибкость элемента λ определяется по формуле

где l_ef – расчетная длина элемента; i – радиус инерции сечения относительно оси, перпендикулярной наибольшей гибкости (плоскости изгиба).

В изгибаемых балках при критическом уровне нагрузки может произойти потеря устойчивости по изгибно-крутильной (общей) форме (поворот сечения относительно его продольной оси). Согласно требованиям [ 1 ] общая устойчивость может быть проверена после определения критического изгибающего момента, который вычисляется по теории тонкостенных стержней в зависимости от величины и места приложения критической нагрузки.

Приближенная оценка устойчивости сжатого пояса изгибаемых балок может быть произведена по формуле (3.5) как для сжатого стержня [ 3 ]. Проверка производится на условную продольную силу:

N = (A_f +A_hcw)σ _cf,

где A_f = b_f∙∙t_f и A_hcw = h_cw∙t_f – соответственно площади сжатого пояса и примыкающего участка стенки; σ _cf – напряжения на уровне центра тяжести сжатого пояса (рис.3.3).

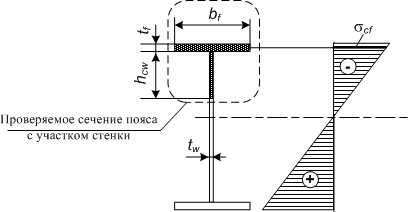
Рис.3.3. Схема к расчету устойчивости пояса

Участок стенки, включаемый в состав пояса, определяется зависимостью:

Радиус инерции i вычисляется с учетом h_cw.

Проверка общей устойчивости разрезной балки и сжатого пояса неразрезной балки не выполняется в случае, если сжатый пояс объединен с железобетонной или стальной плитой.

Расчет местной устойчивости стенок балок выполняют с учетом всех компонентов напряженного состояния σ _x,σ _y и τ _xy (рис.3.4), которые определяются в предположении упругой работы материала по сечению брутто.

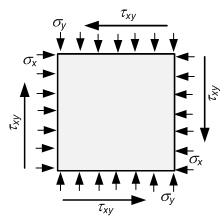
Рис.3.4. Напряженное состояние пластины

Определение значения напряжений σ _x и τ _xy, а следовательно, проверка устойчивости выполняется дважды: при max σ _x и соответствующем τ _xy и при max τ _xy и соответствующем σ _x. Для этогопервый раз загружают временной подвижной нагрузкой линию влияния М на max, и по этой же схеме установки нагрузки загружают линию влияния Q. Второй раз наоборот загружают временной подвижной нагрузкой линию влияния Q на max, и по этой же схеме установки нагрузки загружают линию влияния M.

Максимальное σ _x и минимальное 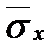нормальные напряжения (положительные при сжатии) по продольным границам пластинки определяются по формулам:

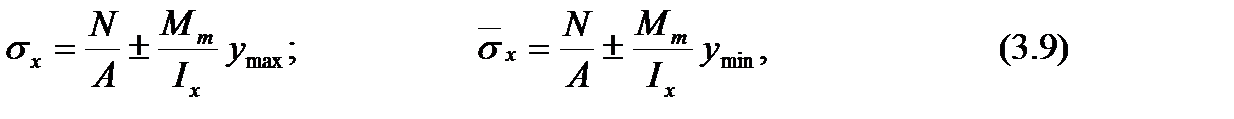
где y_max и y_min – максимальное и минимальное расстояние от нейтральной оси до продольных границ пластинки (с учетом знака).

Среднее касательное напряжение τ _xy определяют по формулам:

а) при отсутствии продольных ребер жесткости

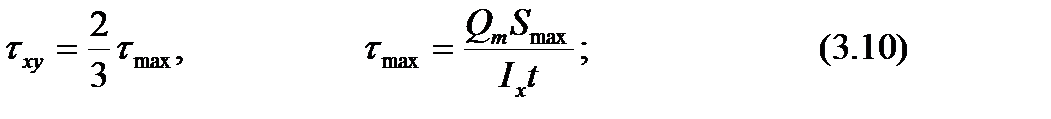
б) при наличии продольных ребер жесткости

В формулах (3.9) и (3.10): M_m и Q_m –средние значения изгибающего момента и поперечной силы в пределах отсека, определяемые по правилам, приведенным в приложении Х [ 1 ]; τ₁ и τ₂ -значения касательных напряжений на продольных границах пластинки (рис.3.5), определяемые по формулам (3.10) при замене S_max соответствующими значениями S.

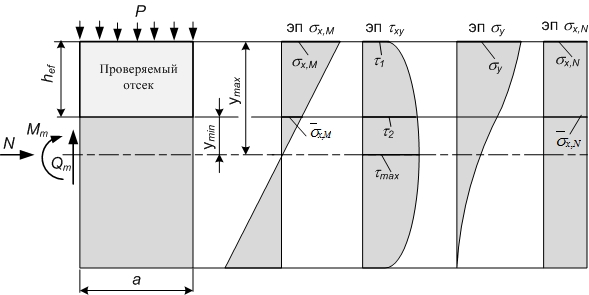
Рис.3.5. Схема к расчету местной устойчивости стенки балки

Поперечное нормальное напряжение σ _y (положительное при сжатии), действующие на внешнюю кромку крайней пластинки следует определять по формуле:

σ _y = (P_q + P _n) /t, (3.12)

где P_q и P _n - распределенные давления на внешнюю кромку пластинки от постоянной и временной нагрузок.

Далее по формулам приложения Х[ 1 ] определяют приведенные критические напряжения σ _x,cr,ef, σ _y,cr,ef и τ _xy,cr,ef, исходя из предположения о неограниченной упругости материла стенки. В основу расчета положена теория устойчивости первого рода для пластинчатых систем. В зависимости от класса стали по прочности и интервала полученных значений приведенных критических напряжений определяют критические напряжения σ _x,cr, σ _y,cr и τ _xy,cr.

Условие устойчивости стенки, подкрепленной только вертикальными ребрами жесткости имеет вид:

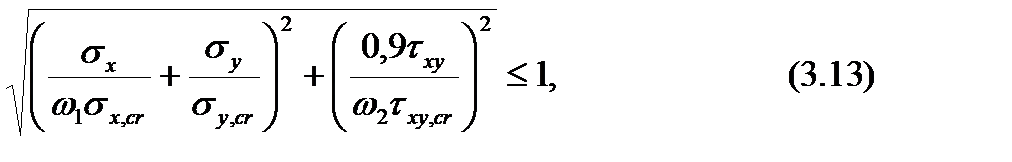
где ω₁ – коэффициент, принимаемый по табл. 3.4 в зависимости от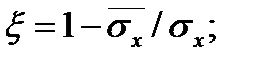

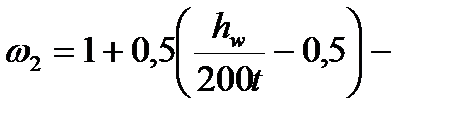
- коэффициент, вводимый при расчете автодорожных и городских мостов при h_w/t > 100.

Таблица 3.4

Значения коэффициента ω₁

ξ		0,5	1,0	1,5	2,0	3,0	4,0
ω1	1,00	1,05	1,10	1,15	1,20	1,30	1,40

Для пластинок, расположенных между сжатым поясом и продольным ребром в сжатой зоне:

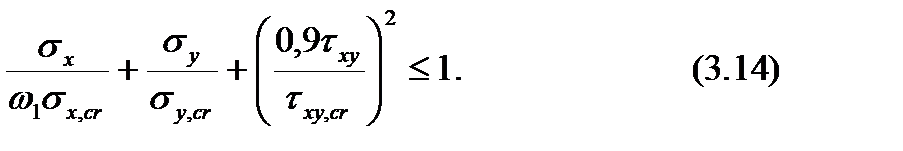
Расчет пластинки растянутой зоны стенки следует выполнять по формуле:

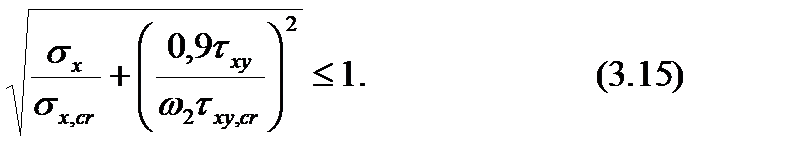
Расчет на выносливость производят на многократно повторное действие нагрузок в их нормативном значении в предположении упругой работы материала по наибольшим нормальным, а для сварных швов – и по наибольшим касательным напряжениям.

Расчетные формулы приведены в п.8.57 [ 1 ].

Дата добавления: 2015-08-17