Численное решение задачи и анализ результатов

Выберем базовые значения параметров (таблица 3.1).

х10	х20	с1	с2	а11	а12	а21	а22
1,5		4,4	5,6	1,4	0,8	1,2	1,9

Рассмотрим случай, когда 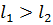и пересекаются (рисунок 2.3):

На рисунке 3.1 приведен график зависимости численности популяции от времени, при базовых параметрах.

Рисунок 3.1 Зависимость численности популяции от времени, при базовых параметрах.

Начальные значения х₁₀ = 1,5 и х₂₀ = 5 соответствуют четвертой области на фазовом портрете (рисунок 2.3).

На данном графике устойчивому состоянию соответствует точка с координатами х₁=2,57 и х₂=1,31. Согласно рисунку 2.3 оба вида сосуществуют, то есть, нет элиминации второго вида.

На рисунке 3.2 приведен график зависимости численности популяции от времени, при значении параметра а₁₁ = 4.

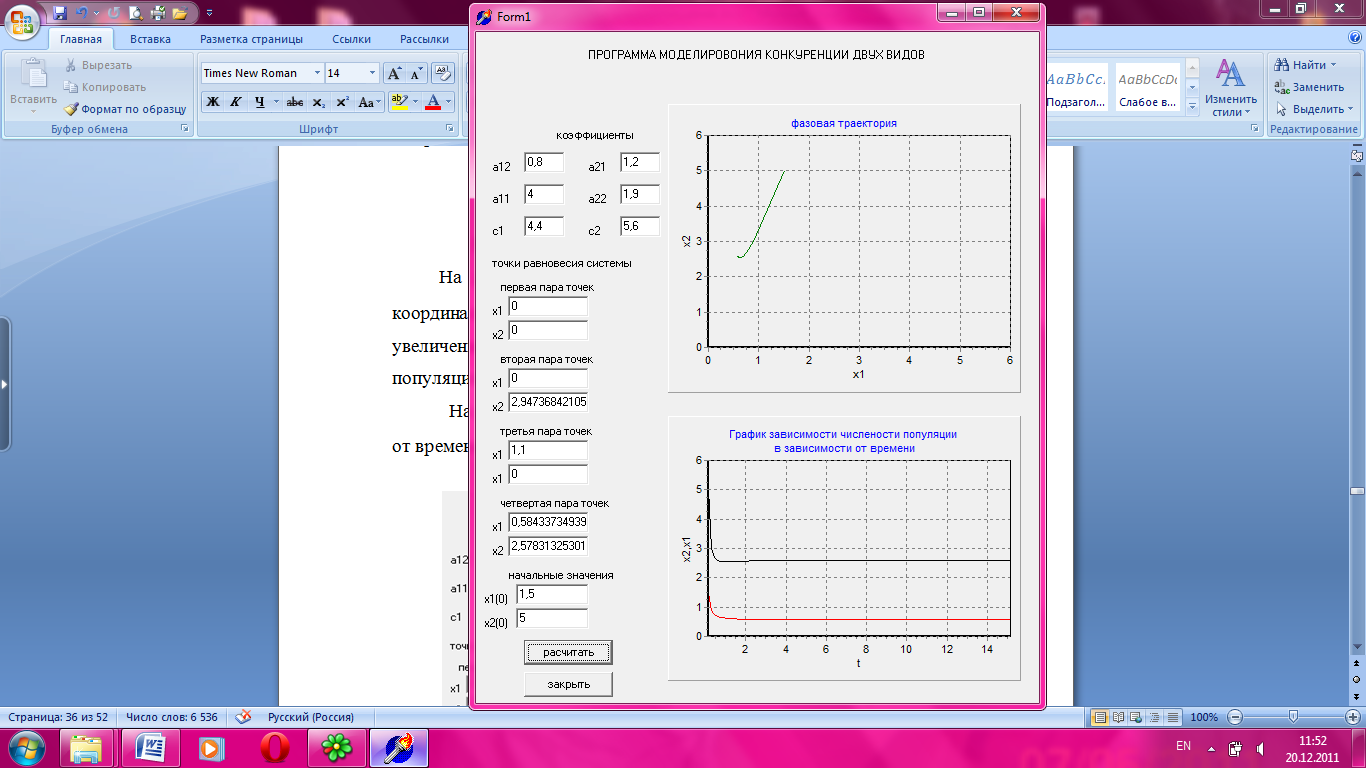
Рисунок 3.2 Зависимость численности популяции от времени.

Увеличение коэффициента 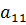приводит к увеличению внутривидовой конкуренции, следствии чего, численность популяции второго и первого вида монотонно снижается и затем принимает постоянное значение, когда достигает устойчивого состояния при х₁=0,58 и х₂= 2,57.

На рисунке 3.3 приведен график зависимости численности популяции от времени, при значении параметра с₁ =6.

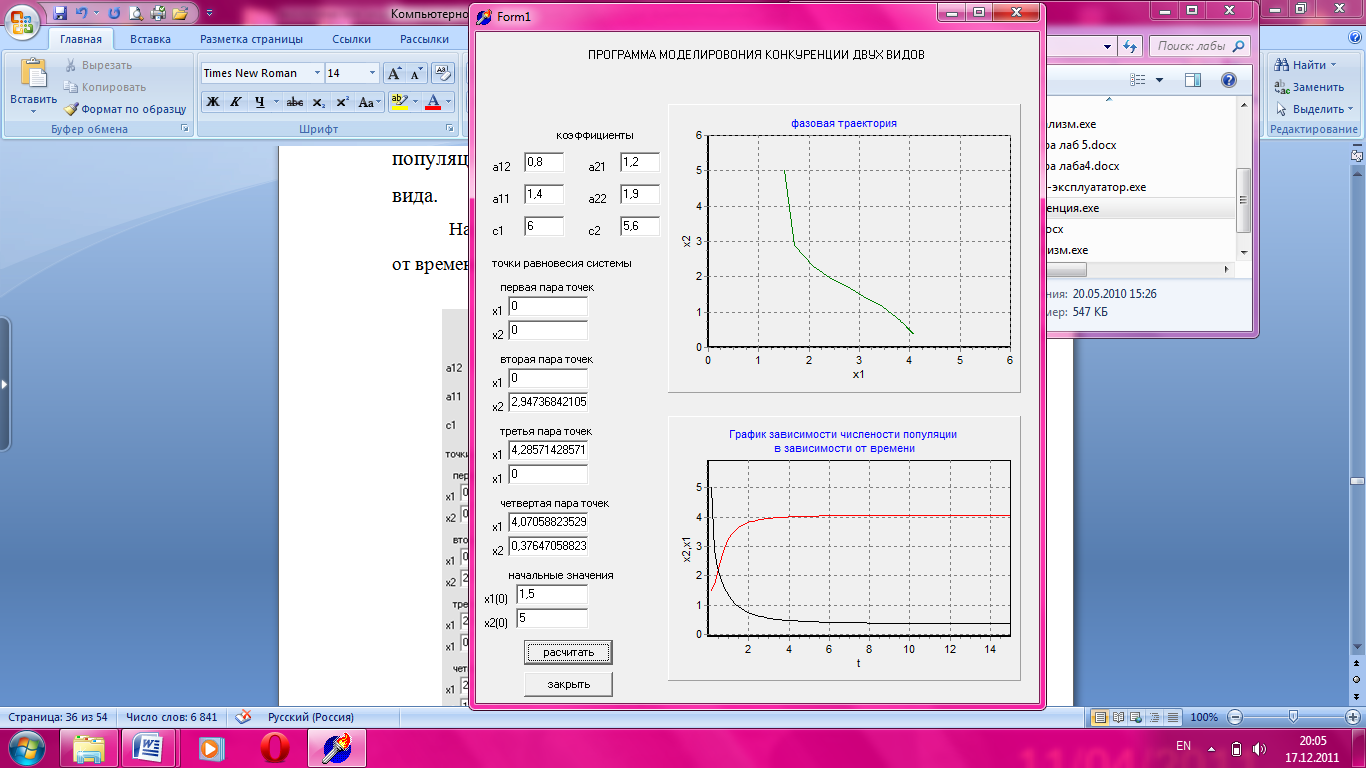
Рисунок 3.3 Зависимость численности популяции от времени

На данном графике устойчивому состоянию соответствует точка с координатами х₁= 4,07 и х₂= 0,376. Это означает, что при увеличении экологической емкости, численность первого вида возрастает и потом принимает постоянное значение, а численность второго вида снижается и затем становится постоянным.

На рисунке 3.4 представлен график зависимости численности популяции от времени, при значении параметра а₁₂ = 0,5

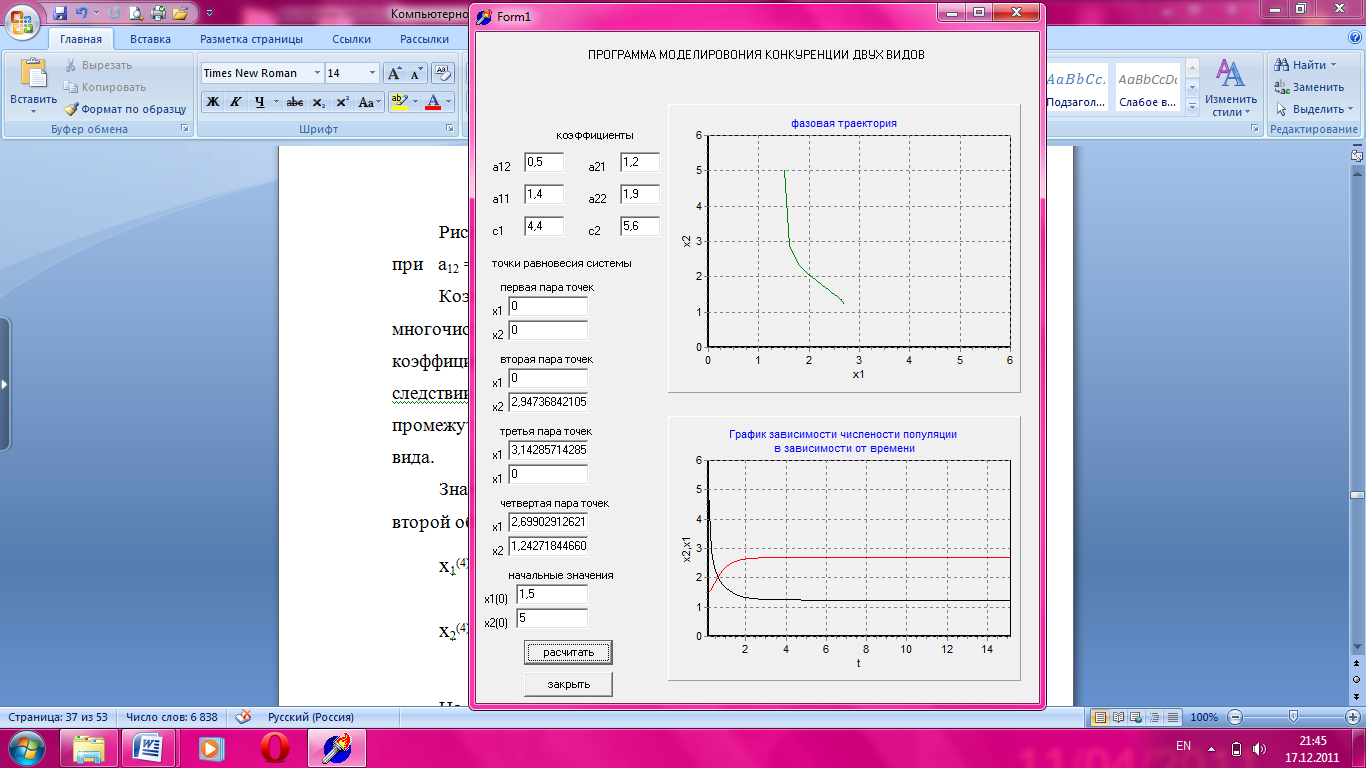
Рисунок 3.4 Зависимость численности популяции от времени.

На данном графике устойчивому состоянию соответствует точка с координатами х₁= 2,69 и х₂= 1,24. Коэффициент а₁₂ показывает межвидовое влияние, и уменьшение этого коэффициента приводит к возрастанию численности первого вида и снижению второго, при этом оба вида сосуществуют.

Рассмотрим пятую область на фазовом портрете (рисунок 2.3) с начальными значениями х₁₀ = 3,5 и х₂₀ = 4,5.

На рисунке 3.5 приведен график зависимости численности популяции от времени, при значении параметра а₂₁ = 0,9 с сохранением значений базовых параметров.

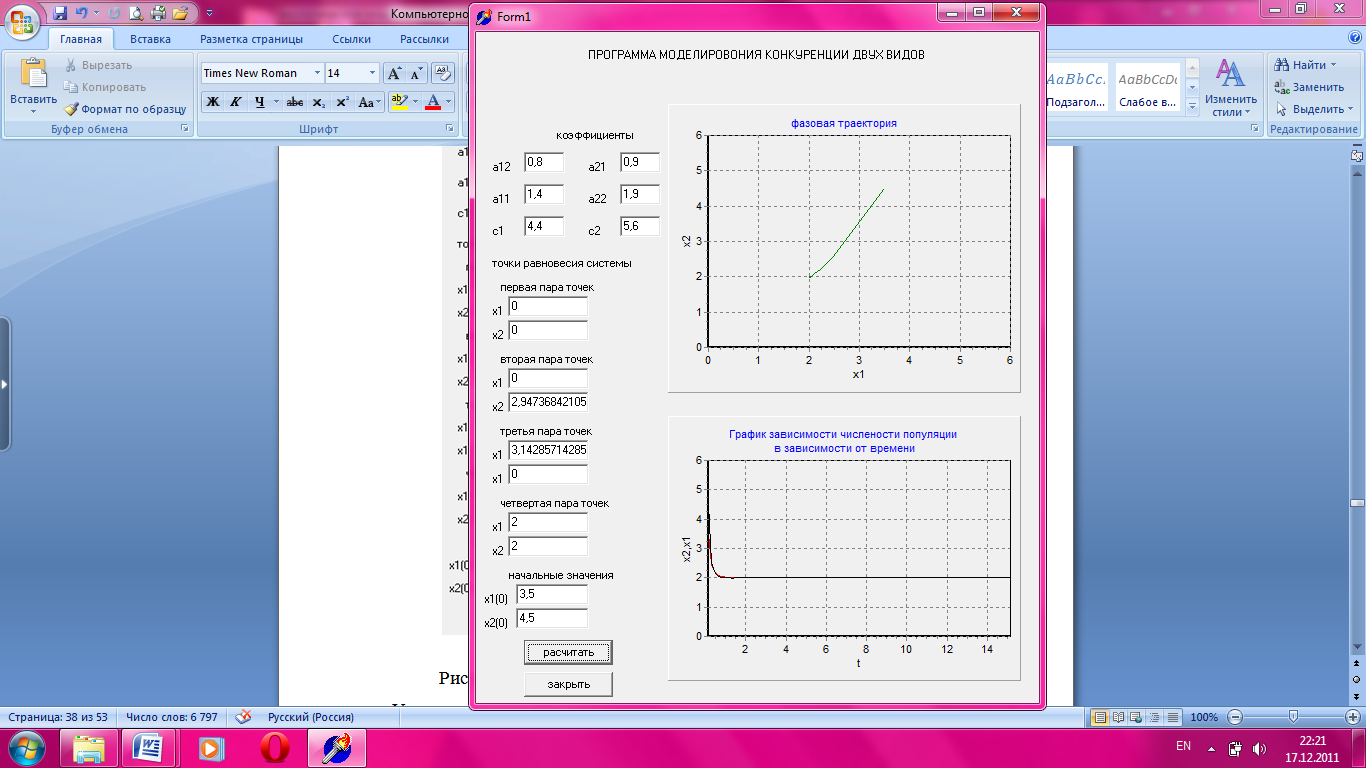
Рисунок 3.5 Зависимость численности популяции от времени.

На данном графике устойчивому состоянию соответствует точка с координатами х₁= 2 и х₂= 2. При уменьшении коэффициента а_21, значение численности обоих видов снижается и принимает постоянное значение.

На рисунке 3.6 приведен график зависимости численности популяции от времени, при значении параметра а₂₂ = 1,3.

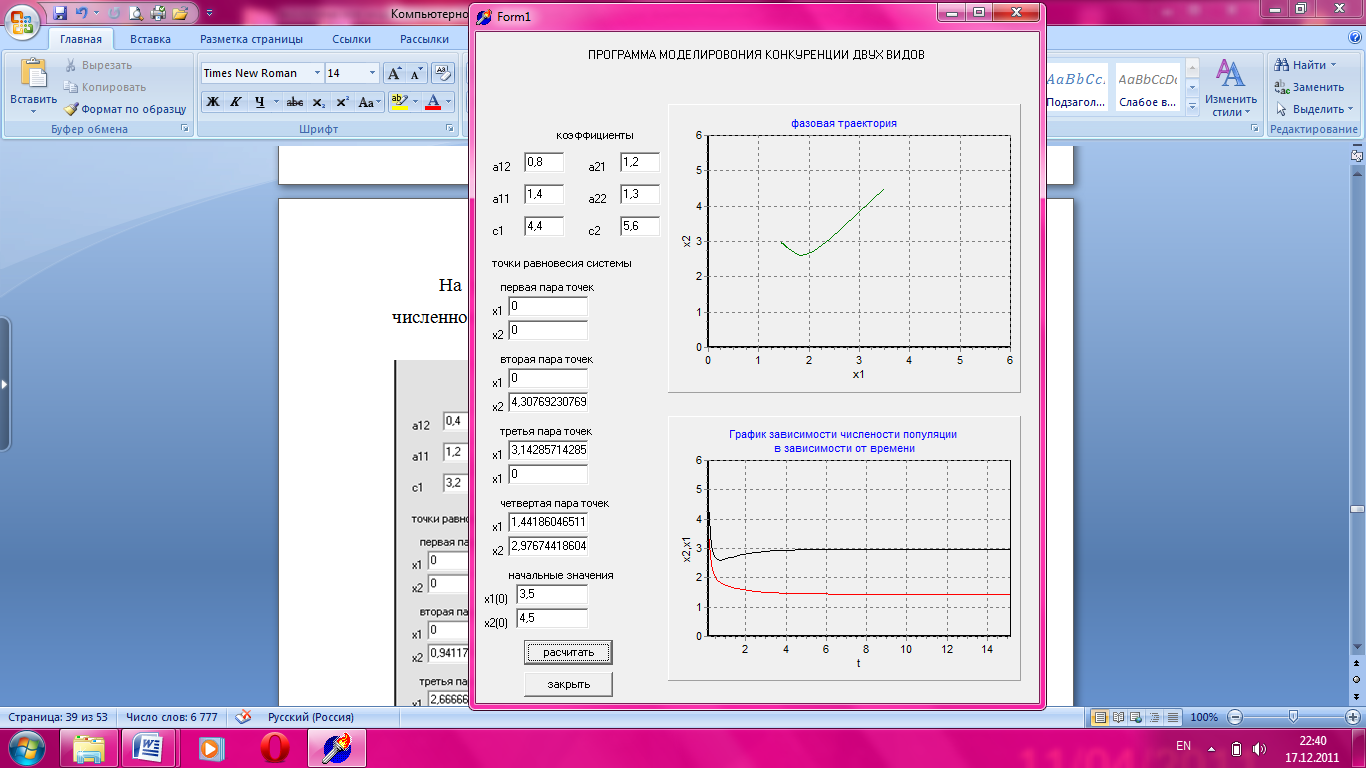
Рисунок 3.6 Зависимость численности популяции от времени.

На данном графике устойчивому состоянию соответствует точка с координатами х₁=1,44 и х₂=2,97. Коэффициент а₂₁ показывает межвидовое влияние, когда малочисленный вид влияет на рост второго вида. Численность второго вида больше численности первого вида.

На рисунке 3.7 приведен график зависимости популяции от времени при значении параметра с₂= 7.

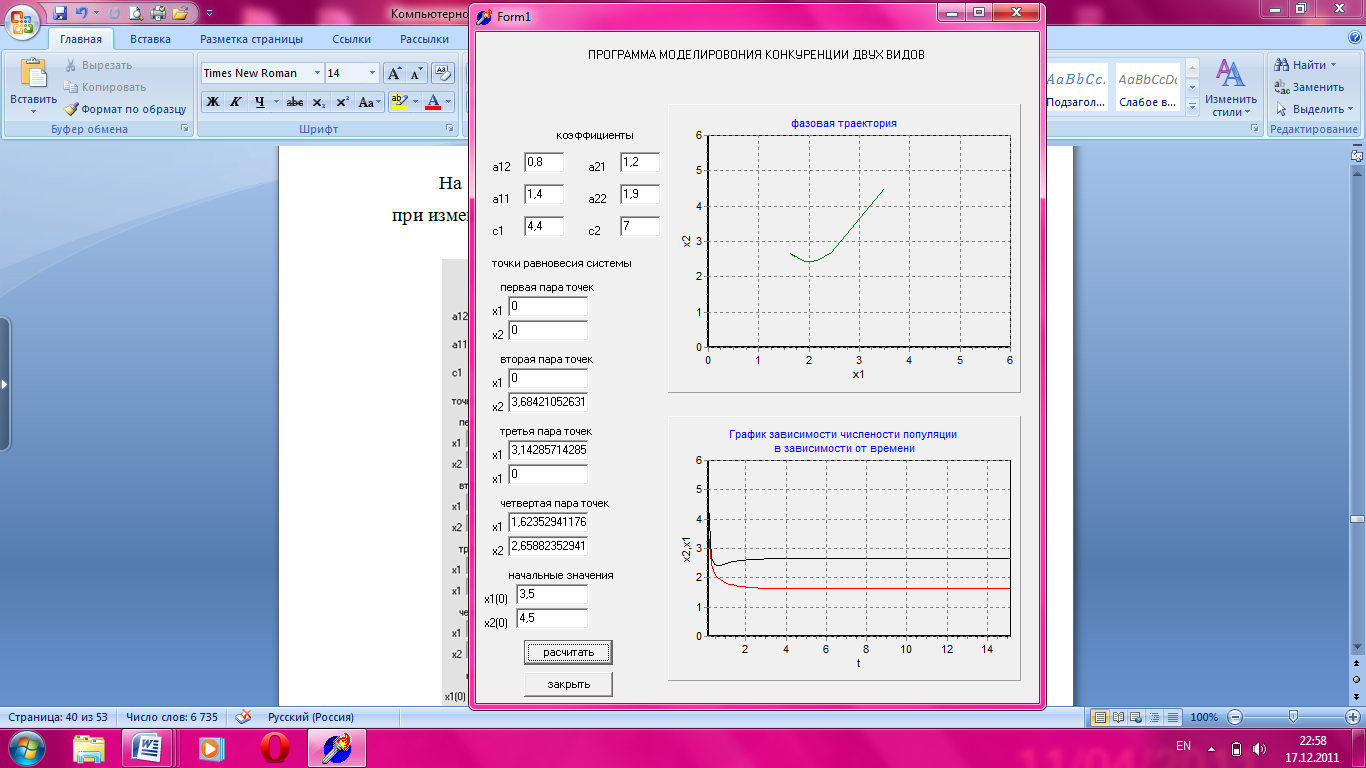
Рисунок 3.7 Зависимость численности популяции от времени.

При увеличении емкости среды происходит снижение численности обоих видов, где в дальнейшем устанавливается устойчивое состояние при значениях х₁=1,62 и х₂=2,65.

Также рассмотрим шестую область на графике изоклин (рисунок 2.3) с начальными значениями х₁₀ = 4,5 и х₂₀ = 1.

На рисунке 3.8 приведен график зависимости численности популяции от времени сохранением остальных базовых параметров.

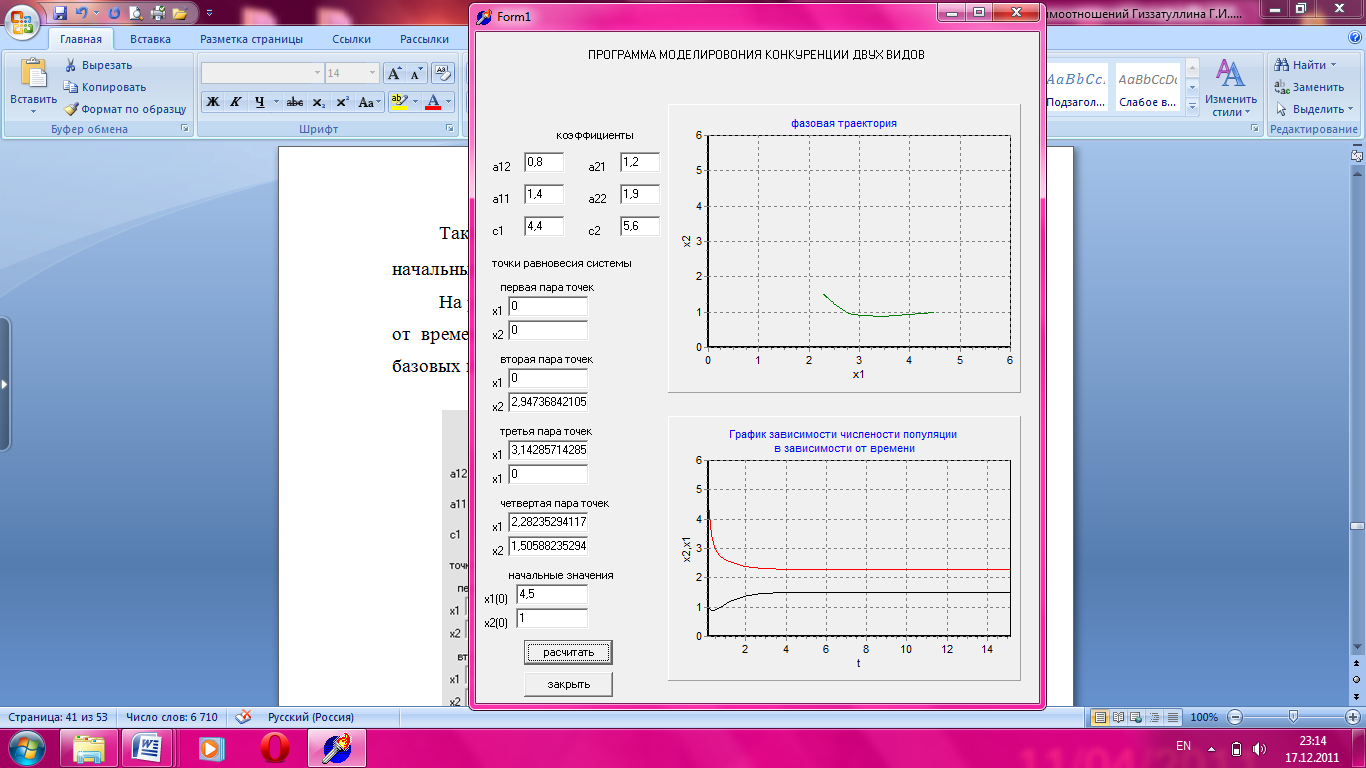
Рисунок 3.8 Зависимость численности популяции от времени.

На данном графике устойчивому состоянию соответствует точка, где х₁=2,28 и х₂= 1,50.Численность первого вида снижается, а численность второго вида возрастает и при этом оба вида сосуществуют.

На рисунке 3.9 приведен график зависимости численности популяции, при значении параметра с₁ = 3 с сохранением остальных базовых параметров.

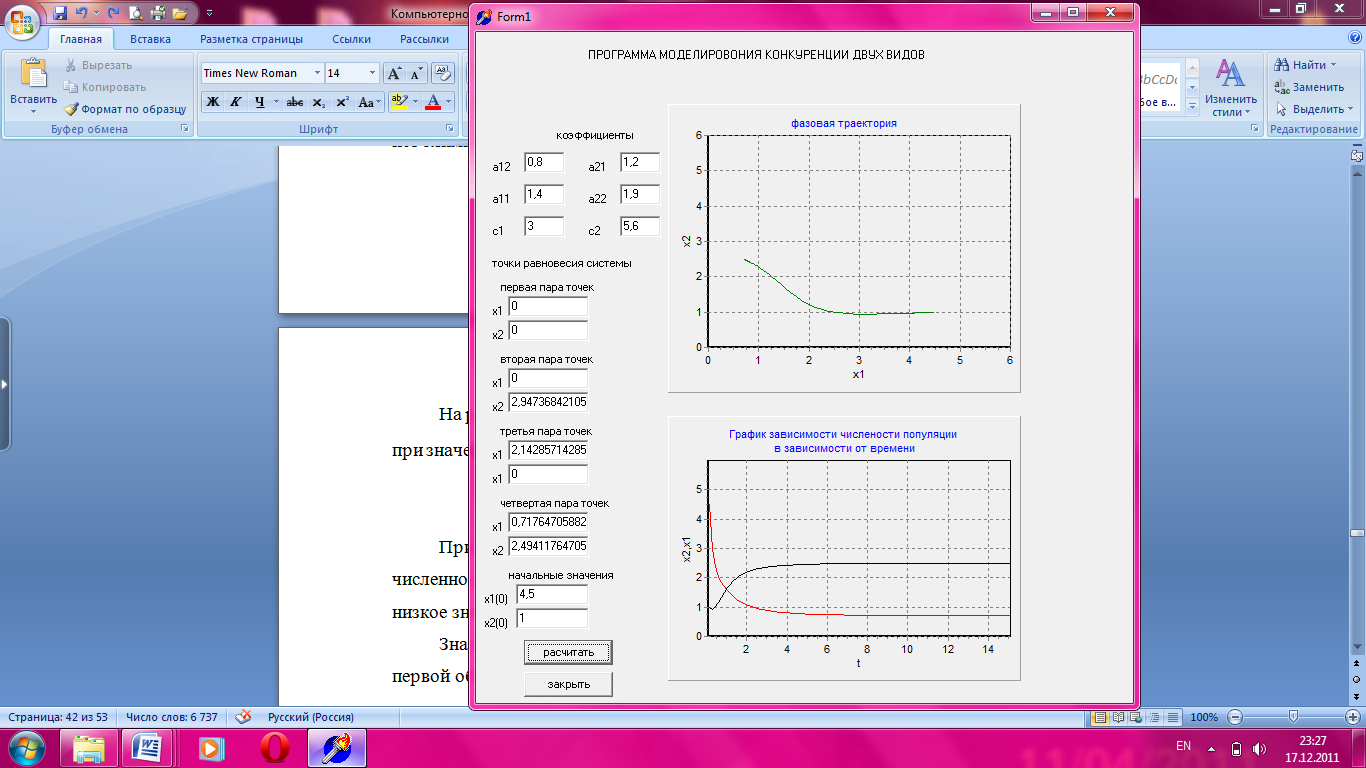
Рисунок 3.9 Зависимость численности популяции от времени.

При уменьшении экологической емкости более слабого вида, его численность быстрее уменьшается, чем при базовых значениях, так как низкое значение экологической емкости всегда влияет на численность видов.

На рисунке 3.10 приведен график зависимости численности популяции от времени при значении параметра а₁₂ = 1,3 с сохранением остальных базовых параметров.

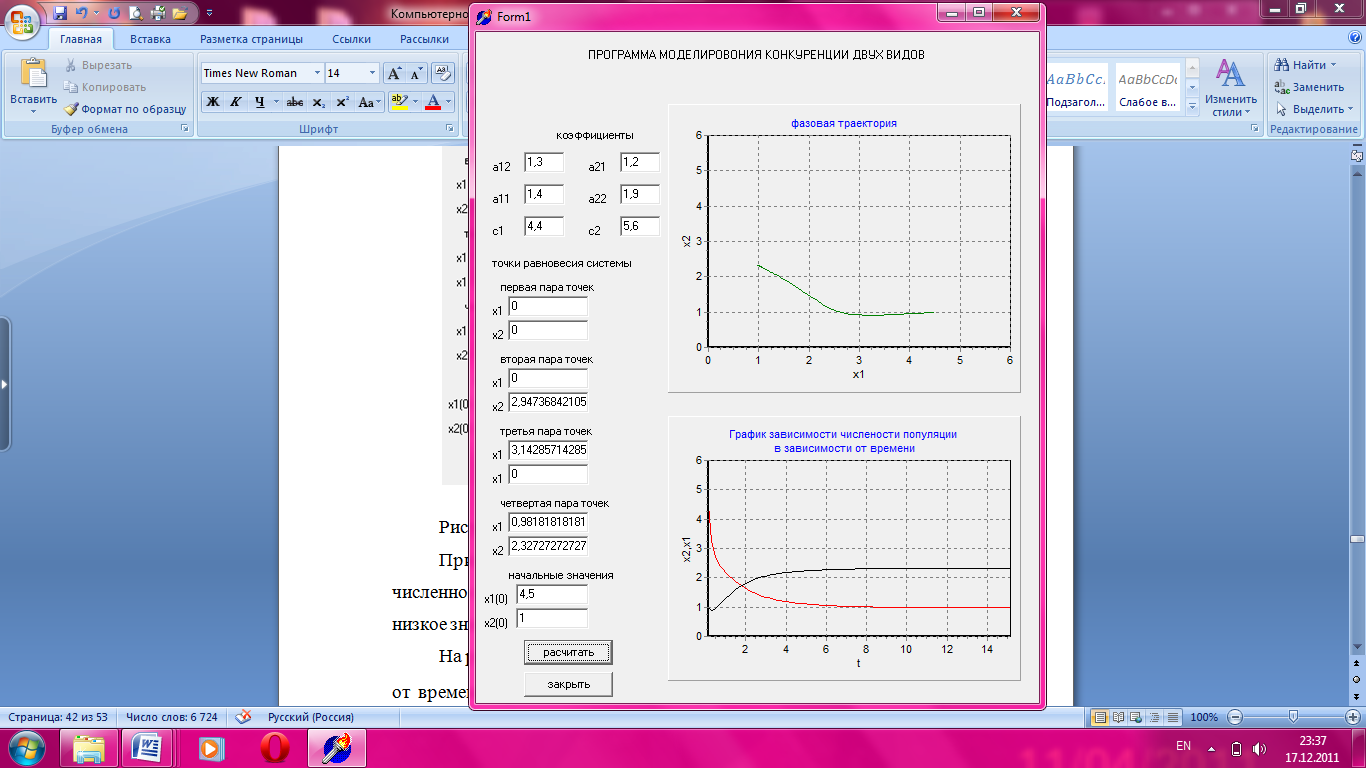
Рисунок 3.10 Зависимости численности популяции от времени.

На данном графике устойчивому состоянию соответствует точка, где х₁= 0,98 и х₂= 2,33. Коэффициент а₁₂ показывает межвидовое влияние, поэтому уменьшение этого коэффициента приводит к возрастанию численности второго вида и снижению первого, при этом оба вида сосуществуют.

На рисунке 3.11 приведен график зависимости численности популяции от времени при значении параметра а₂₁ = 1,4 с сохранением остальных базовых параметров.

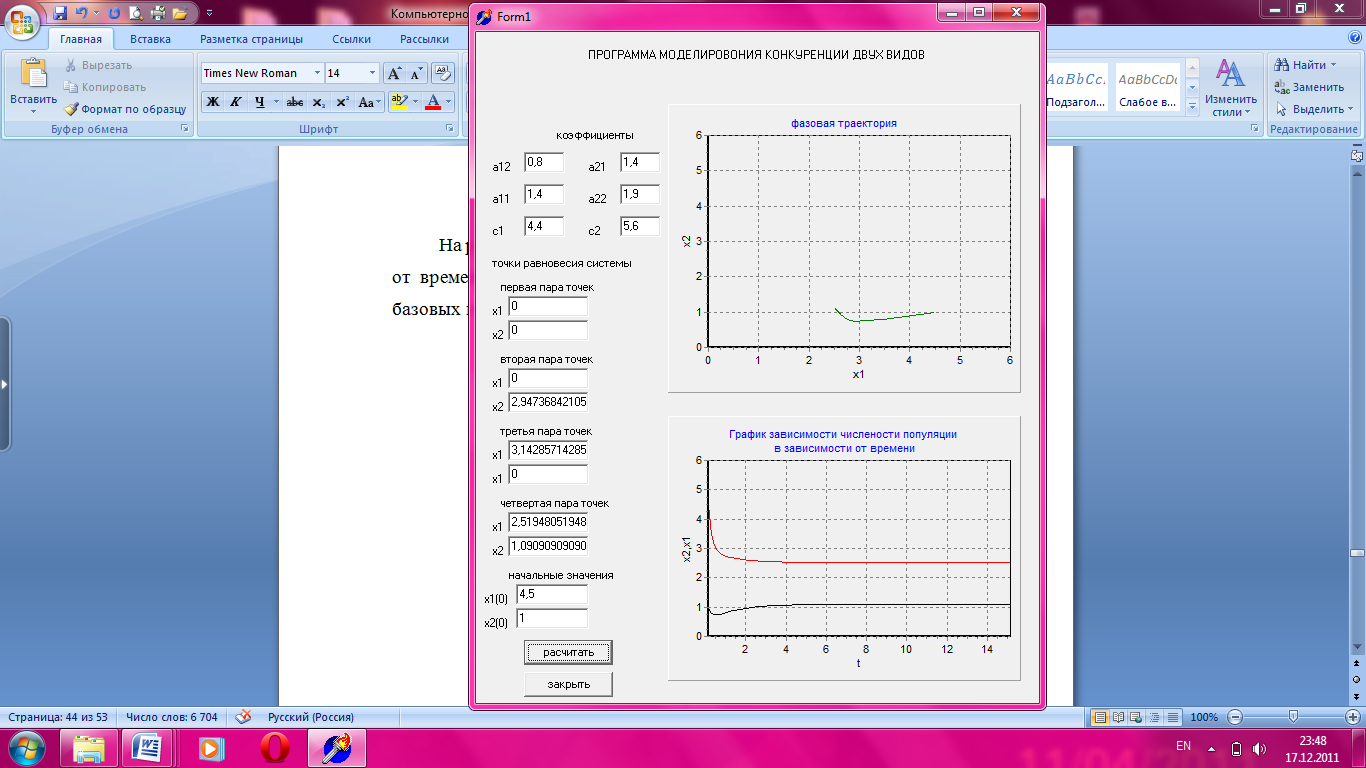
Рисунок 3.11 Зависимости численности популяции от времени.

На данном графике устойчивому состоянию соответствует точка, где х₁=2,51 и х₂= 1,09. При увеличении коэффициента а₁₂ происходит повышении численности второго вида и снижение численности первого.

Заключение

В данной курсовой работе мы исследовали модель межвидовой конкуренции с помощью метода математического моделирования, суть которого заключается в том, что с помощью математических символов строится абстрактное упрощенное подобие изучаемой системы. Далее, меняя значение отдельных параметров, исследуют, как поведет себя данная искусственная система, т. е. как изменится конечный результат.При исследовании межвидовой конкуренции двух видов, мы рассматривали модель, когда горизонтальная изоклина (l₁) выше вертикальной изоклины(l₂) и которые пересекаются.Итак, мы рассмотрели случай, когда оба вида сосуществуют и стремятся к устойчивому состоянию.На основе анализа графиков были сделаны следующие выводы:

1. Вид, у которого более высокая начальная численность имеет больше возможностей выжить в условиях межвидовой конкуренции;

2. Высокая внутривидовая конкуренция углубляет межвидовую конкуренцию;

3. Увеличение экологической емкости популяции увеличивает ее конкурентоспособность.

Список литературы

1. Гринин, А.С. Математическое моделирование в экологии: учебное пособие / А.С.Гринин, Н.А.Орехов. – М.: ЮНИТИ-ДАНА, 2003. – 115с.

2. Кривошеин, Д.А. Экология и безопасность жизнедеятельности: учебное пособие / Д.А.Гринин. – М.:ЮНИТИ-ДАНА, 2000. – 86с.

3. Марчук, Г.И. Математическое моделирование в проблеме окружающей среды. - М.: Наука, 2007.

4. В.В. Алексеев, Т.Г. Сазыкина. Физическое математическое моделирование экосистем. - С. - Петербург: Гидрометеоиздат, 2004.

5. http://hi-bio.narod.ru

6. http://ru.wikipedia.org

Дата добавления: 2015-08-17