
Читайте также:
|
Приравнивая левые части уравнений (1) и (2) находим соответственно уравнения вертикальной и горизонтальной изоклин l1 и l2:
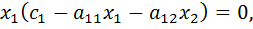
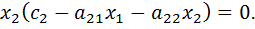
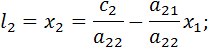
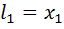 =
= 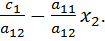
В зависимости от значения коэффициентов может быть:
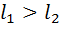 или
или 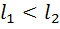
А также при этом изоклины могут пересекаться.
Таким образом, для конкуренции имеем четыре вида фазовых портретов.
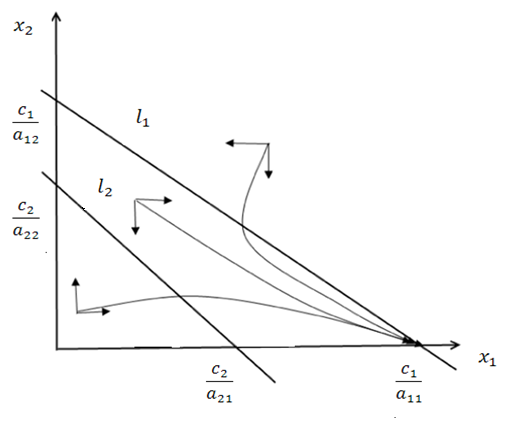
Рисунок 2.1 Фазовый портрет для случая 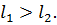
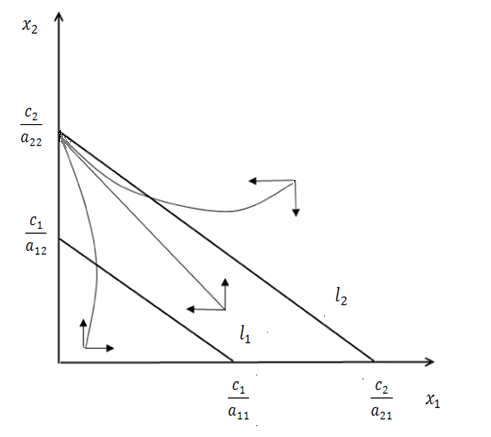
Рисунок 2.2 Фазовый портрет для случая 
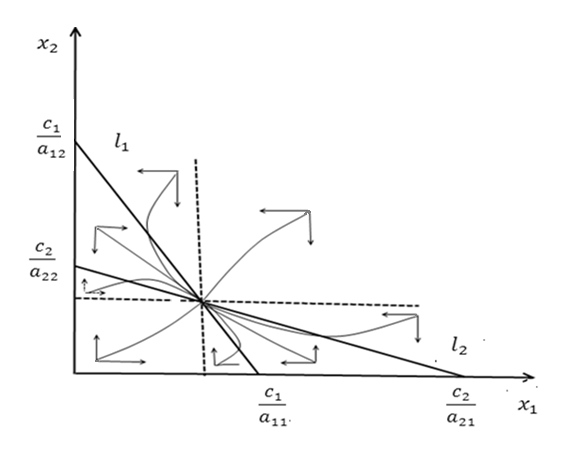
Рисунок 2.3 Фазовый портрет для случая 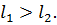
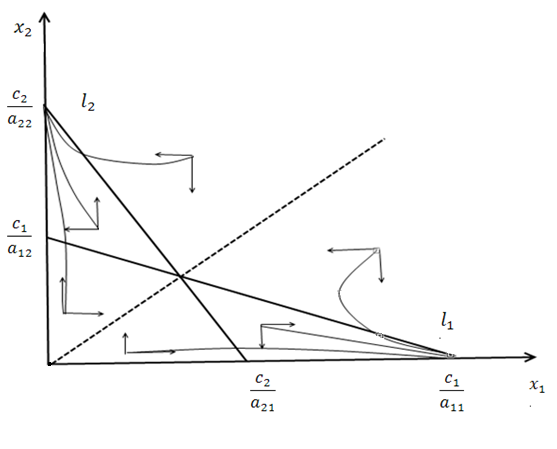
Рисунок 2.4 Фазовый портрет для случая 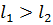
На рисунке 2.1 рассматривается случай, когда численность первого вида монотонно возрастает и затем принимает постоянное значение, а численность второго вида уменьшается и затем совсем исчезает.
На рисунке 2.2 рассматривается случай, когда численность первого вида уменьшается и затем совсем исчезает, а численность второго вида возрастает и затем принимает постоянное значение.
На рисунке 2.3 рассматривается случай, когда оба вида сосуществуют и стремятся к устойчивому состоянию. Точка пересечения изоклин – точка равновесного состояния обоих видов, обладающая локальной устойчивостью (каждый из видов потребляет большее количество того ресурса, который в большей степени ограничивает его собственное развитие).
На рисунке 2.4 рассматривается случай, когда один вид выживает, а другой вид исчезает. Точка пересечения изоклин – точка равновесного состояния, не обладающая локальной устойчивостью (каждый из видов потребляет в больших количествах тот тип ресурсов, который в меньшей степени ограничивает скорость его роста).
Дата добавления: 2015-08-17; просмотров: 83 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Исследование стационарных точек на устойчивость | | | Численное решение задачи и анализ результатов |