
Читайте также:
|
Вид стационарных точек определяется знаком корней 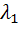 и
и 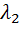 характеристического уравнения:
характеристического уравнения:
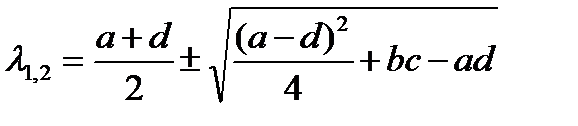 (5)
(5)
Из уравнения (1) и (2) находим:
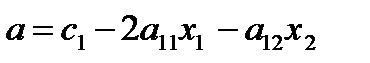 (6)
(6)
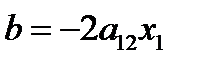 (7)
(7)
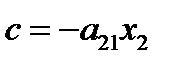 (8)
(8)
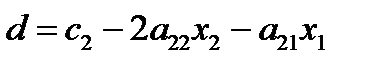 (9)
(9)
1) Рассмотрим первую точку:
х1(1) = 0, х2(1) = 0;
а = с1 , в = 0, с = 0, d = c2 .
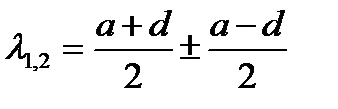 ; (10)
; (10)
l1= a; l2 = d;
l1= c1> 0; l2= c2 > 0.
Таким образом, для первой точки корни характеристического уравнения положительные числа, поэтому эта точка есть «неустойчивый узел».
Вывод: В результате конкуренции оба вида друг друга не уничтожают полностью.
2) Вторая особая точка:
х1(2) = 0, 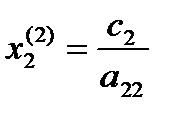
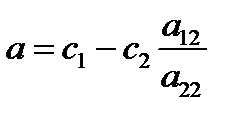 , в = 0,
, в = 0, 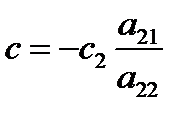 ,
, 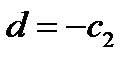 .
.
l1= a; l2 = d.
если 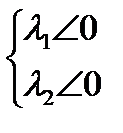 , то
, то 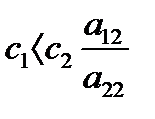 .
.
Таким образом, вторая точка является «устойчивым узлом».
если 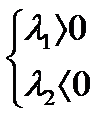 , то
, то 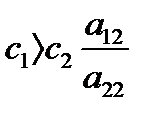
При этом образуется неустойчивая точка – «седло».
3) Третья особая точка:
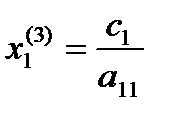 , х2(3) =0.
, х2(3) =0.
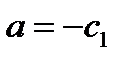 ,
, 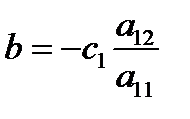 , с = 0,
, с = 0, 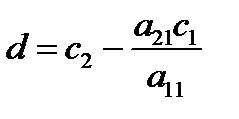 .
.
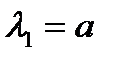 ;
;
l1= -c1< 0 l2 <0.
Если 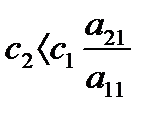 , то «устойчивый узел», если
, то «устойчивый узел», если 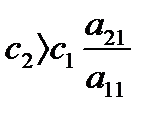 , то «седло».
, то «седло».
4) Четвертая особая точка определяется сосуществованием двух конкурирующих видов («устойчивый узел») при выполнении условия:
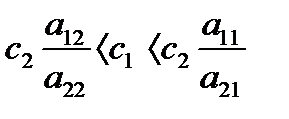
Дата добавления: 2015-08-17; просмотров: 57 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Постановка задачи | | | Построение фазового портрета |