Линейная регрессия

Рассмотрим реализацию метода наименьших квадратов применительно к уравнению вида

y = ax + b.

Графическая иллюстрация аппроксимации представлена на рисунке.

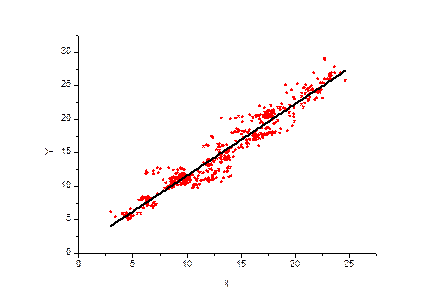
Здесь точки – результат эксперимента, а прямая – результат линейной регрессии.

Для нахождения коэффициентов а, b искомой прямой необходимо минимизировать сумму квадратов расстояний Dy_i по ординате от точки (х_i; y_i) до прямой. Цель - определить коэффициенты a и b таким образом, чтобы величина

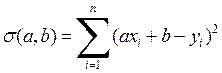
приняла наименьшее значение.

Известно, что для поиска экстремумов гладких функций нескольких переменных нужно находить критические точки, т.е. те точки, в которых все частные производные функции равны нулю. В нашем случае необходимо решить следующую систему:

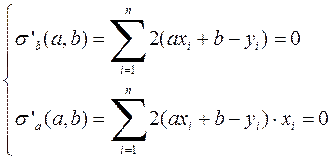
Это система двух линейных уравнений с двумя неизвестными a и b.

Перепишем ее в следующем виде:

Получим систему нормальных уравнений метода наименьших квадратов.

Введем стандартные в статистике обозначения для моментов:

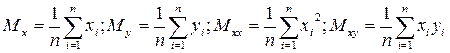
Тогда наша система перепишется в следующем виде:

,

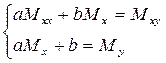которая решается, например, методом Крамера.

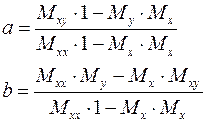
Разберем пример нахождения наилучшей линейной функции.

Пусть зависимость задана таблицей

x	-3	-1
y

Для вычисления моментов M_x, M_y, M_xx, M_xy построим таблицу:

	x	y	x^2	xy
	-3			-9
	-1			-4
Сумма
Среднее значение (М)		6.2		13.4

Отсюда получаем систему

9a+b=13.4 a=0.9

a+b=6.2 или b=5.3

Итак, наилучшая линейная функция имеет вид y=0.9x+5.3.

Упражнение. Проверьте, что если исходные данные удовлетворяют линейной зависимости y_i=а·x_i+b, то и коэффициенты a и b, полученные при решении указанным методом совпадут с исходными.

Дата добавления: 2015-08-20