Потенциальная помехоустойчивость оптимального приемника двоичных частотно-модулированных сигналов с неизвестной начальной фазой

Рассмотрим прием ЧМ сигналов с неизвестной начальной фазой (см.рис.7.15). ЧМ сигналы являются ортогональными и для них выполняется условие:

(7.50)

Рассмотрим случай, когда на входе присутствует сигнал u ₁(t). Отклик первого согласованного фильтра в момент окончания первого единичного интервала не равен нулю (см. рис.7.15, б), а отклик второго согласованного фильтра в этот же момент времени равен нулю, так как ЧМ сигналы ортогональны, и отклик второго согласованного фильтра на сигнал u ₁(t), определяемый уравнением (7.50), равен нулю.

Огибающая смеси сигнала и шума на выходе первого детектора больше огибающей смеси сигнала и шума на выходе второго тот же момент времени t_и, т.е.

При выполнении последнего неравенства демодулятор принимает правильное решение, а при его невыполнении возникает ошибка.

Пусть случайные величины ξ₁, ξ₂определяются двумерной плотностью вероятности w (J₁,J₂)Зная эту плотность и условие, при котором возникает ошибка, можно вычислить ее вероятность:

(7.51)

Вероятность события, заключающегося в том, что реализация огибающей смеси сигнала и шума на выходе первого канала меньше реализации огибающей шума на выходе второго канала

Вероятность ошибки определяется всеми подобными событиями. Плотность вероятности w (J₁) определяется формулой (4.44), а плотность w (J₂/J₁) - формулой (4.43). Входящая в эти формулы дисперсия σ²=0, 5 N₀E, где

— энергия сигнала.

Подставляя формулы (4.43), (4.44) в формулу (7.51) и производя вычисления, получим выражение для вероятности ошибки

(7.52)

где h² =E/N₀— отношение энергии элемента к спектральной плотности мощности шума.

Аналогичное выражение имеет и вероятность P (u ₁/ u ₂). Окончательное выражение для вероятности ошибки при приеме равновероятных ЧМ сигналов со случайной начальной фазой

(7.53)

Эта формула справедлива и для других ортогональных сигналов с одинаковой энергией.

Потенциальная помехоустойчивость оптимального приемника двоичного амплитудно-модулированного сигнала с неизвестной начальной фазой

В данном случае вероятность ошибки

где

w (J/1) - плотность распределения вероятности огибающей на выходе оптимального приемника (амплитудного детектора) в момент времени t = t_и, совпадающий с окончанием единичного интервала (эта плотность определяется формулой (4.44));

w (J/0)- аналогичная плотность распределения вероятности, определяемая формулой (4.43);

u _п- пороговый уровень.

Для P (1) = P (0) = 0,5 выражение для вероятности ошибки [25]:

(7.54)

Минимальная вероятность ошибки получается при оптимальном значении u _п. Оно находится из уравнения

dp/ du _п = 0.

Можно показать, что

Подставляя оптимальное значение порогового уровня в (7.54), получим окончательное выражение для вероятности ошибки при большом отношении сигнал/шум.

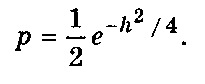
Дата добавления: 2015-08-20