Системы с неполнодоступным включением серверов.

Системы с несколькими серверами могут по-разному распределять их ресурс для обслуживания поступающих заявок. Если любой свободный сервер может обслуживать любую поступающую заявку, то говорят о полнодоступном включении серверов. Если за определенными серверами закрепляются заявки, поступающие только с определенных входных линий, то говорят о неполнодоступном включении серверов (НВ).

В уравнениях Чепмена-Колмогорова неполнодоступность можно отразить введением специальной функции, зависящей от состояния системы, значение которой определяет вероятность получения доступа к серверу. Иначе говоря, речь идет о том, что вероятность блокировки в неполнодоступных схемах включения серверов зависит не только от количества серверов, но и от способа их включения для обслуживания, т.е. определяется вероятностями занятия определенных, а не любых серверов.

Обозначим:

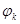- функцию состояния k, значение которой равно вероятности обслуживания заявки, поступившей в СМО в этом состоянии. Стационарное распределение вероятностей в этом случае будет зависеть как от параметра входного потока, так и от значения .

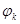Диаграмма интенсивностей переходов для СМО с m серверами, явными потерями и неполнодоступным включением изображена на рисунке 1.21:

Рис. 1.21 Диаграмма интенсивностей переходов для СМО с m серверами, явными потерями и неполнодоступным включением.

Запишем уравнения баланса

.

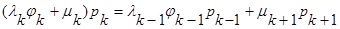Для нашего случая входной поток пуассоновский и можно положить

Тогда решение для стационарного распределения вероятностей состояний дается формулой

Полученное выражение называют третьим распределением Эрланга. Рассмотрим вероятность блокировки в такой системе. Очевидно, что если все

, то все состояния доступны и блокировка будет опреде­ляться известной B-формулой Эрланга, в которую перейдет полученное выше третье распределение Эрланга.

При ином задании функции 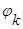вероятность блокировки будет определяться иначе. Вероятность потери вызова, поступившего в систему, находящуюся в состоянии k по определению равна .

Вероятность потери вызовов в среднем по всем состояниям, которая для нашего случая будет совпадать с вероятностью потерь по времени, тогда определится формулой

.

Интенсивность обслуженной нагрузки в такой СМО может быть рассчитана:

.

Очевидно, что зависимость j_i определяется способом подключения серверов к обслуживаемым линиям, которых обязательно должно быть больше двух, иначе неполнодоступное включение теряет смысл. В общем случае в неполнодоступной схеме выделяют нагрузочные группы - полнодоступные коммутационные системы, обеспечивающие подключение любого из n -входов к D -выходам, и объединительную схему, представляющую собой набор сумматоров в аналоговой схемотехнике или набор логических «или» в цифровой. В старых АТС объединительная схема реализуется в виде простых «монтажных или» в промежуточном щите переключений (ПЩ).

Если считать, что имеется g -нагрузочных групп с D выходами каждая (см. рис. 1.22.), то объединительная схема должна распределять gD выходов нагрузочных групп по m серверам (выходным линиям) фиксированным образом, т.е. часть выходов нагрузочных групп должна объединяться и подключаться к одному и тому же серверу (выходной линии).

Рис. 1.22 Система с неполнодоступным включением.

Параметр D называют доступностью нагрузочной группы. В симметричных неполнодоступных (н.д.) схемах значения n и D одинаковы для всех групп, а в асимметричных эти значения могут различаться. Асимметричные схемы практически не поддаются расчету. Задача построения эффективной схемы НВ сводится к определению объединительной схемы, т.е. способа подключения определенным образом m выходных линий к полю из gD выходов нагрузочных групп.

Необходимым условием реализации НВ является неравенство: .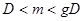

Если m = D – это одно полнодоступное включение

Если m = gD – это g полнодоступных включений.

Важной характеристикой НВ является коэффициент уплотнения: .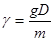

Его значение определяет сколько в среднем выходов различных нагрузочных групп подключено к одному серверу (линии).

При γ < 2 слабая связность и схема имеет низкую пропускную способность

На практике наиболее частоприменяют 2 < γ < 6.

Большие значения γ (γ > 6) не увеличивают пропускную способность значи­тельно, тогда как сложность сильно возрастает.

По структуре объединительной схемы различают равномерный и ступенчатый способы объединения.

При ступенчатом способе с ростом номера сервера растет число обслуживаемых линий, при равномерном обслуживаемые линии распределяются между серверами равномерно по числу γ на каждый или по γ+1 для некоторых.

Рассчитать равномерное образование можно, найдя представление числа γ в виде:

Здесь квадратными скобками обозначена целая часть числа.

При этом m₁ серверов будут обслуживать [γ]+ 1 линий, а m₂ –серверов [γ] линий.

Различные примеры схем НВ показаны на рис. 1.23.

Каждой схеме НВ можно поставить в соответствие матрицу связности

Элементы главной диагонали матрицы указывают значение доступности.

Каждый элемент на пересечении i -строки и j - столбца указывает на число связей между i -ой и j -ой группами.

.

Матрица связности определяет оптимальную схему НВ, если

.

Первое условие называют условием качества перехвата, а второе условием качества перекоса.

Практически приемлемые условия качества перехвата и перекоса можно легко получить, используя специфическую структуру равномерной схемы, называемой «цилиндр». На рис.1.23. это схемы г) и е). Для схем типа цилиндр матрица связности циклична и m = g. Величина γ = r, которую называют числом шагов цилиндра.

Схема 1.23. е) представляет собой пять двухшаговых цилиндров, а схема 1.23.г) – два одношаговых, два двухшаговых и один четырехшаговый.

Для цилиндров рассчитывается только одна строка, поскольку все остальные получаются циклическим сдвигом.

Анализ показывает, что среди эквивалентных по матрицам связности цилиндров можно выбрать несколько типовых схем, для которых рассчитываются все параметры. Такие схемы сведены в таблицы. Используя эти таблицы, проводят синтез объединительных схем для НВ. Более лучших результатов можно добиться использованием специальных компьютерных программ.

Теперь вернемся к аналитическому описанию СМО и определению функции φ.

Если доступность НВ равна D. То следует положить .

Рис. 1.23 Виды схем неполнодоступных включений.

Для так называемой идеально симметричной схемы включения (ИСС), при которой каждой нагрузочной группе доступна своя, отличная от других комбинация D серверов, можно определить функцию φ достаточно просто. Поскольку число различных комбинаций из D серверов при общем их числе m определяется числом сочетаний .

Вероятность занятия фиксированных i серверов будет определяться

.

Например, для схемы на рис. 1.24 D=2,m=4,

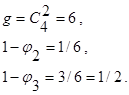
Рис.1.24 Идеально симметричная НВ.

Для других отличных от ИСС схем НВ задание функции φ более сложно. Однако расчет пропускной способности произвольной схемы НВ ведут, опираясь на формулы для ИСС, если γ >2. Для приближенных расчетов выведен целый ряд формул, которые сыграли большую роль при проектировании узлов коммутации, когда применение компьютеров было сильно ограниченным. И сейчас они играют большую роль для эскизных расчетов.

На рис. 1.25 приведены результаты расчета коэффициента использования линии (сервера):

.

В предположении ИСС для различных значений g, D =10, p_B =0.003.

Характерно, что с ростом числа серверов использование линии сначала увеличивается, а затем уменьшается. В крайних точках m=g и m=gD использование линии одинаково, так как соответствует полнодоступному включению.

Рис. 1.25 Среднее использование линии m в НВ в зависимости от емкости пучка m при различных значениях g, D=10 и P=0.003.

Важной практической характеристикой СМО с несколькими серверами является единичное приращение интенсивности обслуженной нагрузки при увеличении числа серверов на единицу и постоянной норме потерь - вероятности блокировки. Эту величину называют единичным приращением

.

Для полнодоступных систем при постоянной вероятности блокировки и постоянном числе входных линий из полученных ранее формул для обслуженной нагрузки следуют неравенства:

Это неравенство говорит о том, что удвоение числа серверов увеличивает пропускную способность системы более чем вдвое. Рис. 1.26 показывает зависимость единичного приращения от числа серверов в полнодоступной системе при фиксированной вероятности блокировки. Для неполнодоступных систем рост единичного приращения от числа серверов заметно меньше, чем для полнодоступной.

Рис. 1.26 Зависимость единичного приращения Dy_u от числа выходов m при обслуживании простейшего потока и различных вероятностях потерь Р_В.

При переходе от схемы ПВ к схеме НВ значение единичного приращения скачкообразно уменьшается.

Эскизные расчеты схем НВ могут проводиться с помощью приближенных формул. Известна формула О’Делла, позволяющая оценить необходимое число серверов m при неполнодоступной схеме их включения с доступностью D по заданной обслуженной нагрузке Y и вероятности блокировки:

.

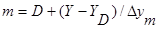Здесь используется базовая величина для обслуженной нагрузки D серверами.

Коэффициент использования сервера при γ =1:

.

С ростом γ, величина единичного приращения увеличивается, как было пока­зано, для ИСС можно считать .

Пусть на некоторую ИСС поступает γ пуассоновских потоков интенсивностью b=λ/gD каждый. С ростом m число потоков:

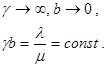
Вероятность занятия одного фиксированного сервера тогда может быть задана величиной в точности равной η=Y/m. Для D фиксированных серверов эта вероятность будет очевидно η^D. Для схем НВ эта вероятность в точности равна p_B. Следовательно, приходим к соотношениям

В некоторых странах принято использовать формулу Пальма -Якобеуса для определения обслуженной нагрузки и вероятности блокировки. Она представляет собой систему нелинейных уравнений следующего вида

Здесь используется функция Эрланга, определенная ранее.

---

Дата добавления: 2015-08-02