|
Читайте также: |
Найдем теперь вероятность занятия определенных, выбранных заранее серверов. Эта задача часто встречается при определении нагрузки на определенные выходы в коммутаторах каналов телефонных сетей. Будем исходить из того, что в результате применения модели Эрланга или Энгсета или Бернулли найдены вероятности занятия любых k серверов pk.
Зафиксируем определенные i серверов из m доступных. Предположим, что занятие серверов происходит равновероятно. Тогда если в системе с вероятностью 
занято точно i + j серверов, то вероятность занятия одной конкретной комбинации будет в число таких сочетаний раз меньше, т.е. 
.
Поскольку отмеченные i серверов могут быть заняты совместно с любыми другими j серверами в соответствующем числу сочетаний из m по j комбинациях, где j любое число от 0 до m-i, то можно получить формулу для вероятности занятия фиксированных i серверов в системе с M входами:
.
Для модели Эрланга тогда получим:
.
Для модели Энгсета формула будет отличаться:
.
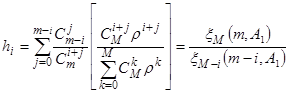Для системы с одинаковым числом входов и выходов (серверов) имеет место модель Бернулли и соответствующие вероятности занятия фиксированных серверов будут:
.
Дата добавления: 2015-08-02; просмотров: 96 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Анализ систем массового обслуживания с марковскими потоками требований. | | | Модель Эрланга Модель Энгсета |