Анализ систем массового обслуживания с марковскими потоками требований.

В этом разделе вы познакомитесь с методами расчета характеристик качества обслуживания QоS систем массового обслуживания, если они могут быть описаны моделью с марковским потоком требований на входе, т.е. интервалы времени между поступлениями соседних требований являются случайной величиной с экспоненциальным распределением.

1.3.1 Система М/M/1. Анализ.

Как было описано при классификации систем, это система с пуассоновским входным потоком заявок, экспоненциальным законом распределения времени обслуживания и одним сервером.

На рис. 1.10 приведена простейшая схема такой системы. Она содержит буфер, который может хранить очередь бесконечной длины, состояние которой может быть отождествлено с числом заявок, содержащихся в очереди в каждый момент времени.

Рис. 1.10 СМО типа М/М/1.

Поскольку входной процесс ординарный, то в каждый момент времени к очереди может добавиться только одна заявка, поскольку сервер один, то в каждый момент времени может быть обслужена, то есть уйти из очереди только одна заявка. Таким образом, рассматриваемая СМО относится к процессу класса «гибели-размножения». Для анализа необходимо конкретизировать параметры системы. Распределение вероятностей входного потока и времени обслуживания позволяет полагать интенсивности вероятностей в модели постоянными.

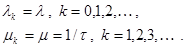
Здесь t – среднее время обслуживания в сервере.

На рис 1.11 приведена диаграмма интенсивностей переходов для рассматриваемой системы.

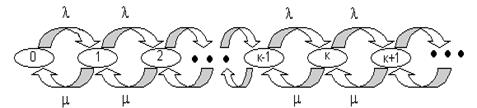
Рис. 1.11 Диаграмма интенсивности переходов для СМО типа М/М/1.

Полученное ранее общее решение позволяет сразу записать вероятность того, что в стационарном состоянии в очереди будет находиться k заявок

Найдем начальное значение вероятности, учитывая сходимость соответствующего ряда

.

Окончательно получаем формулу для вероятности длины очереди

.

На рис. 1.12 приведен график вероятностей того, что в очереди находится k заявок в установившемся режиме.

Рис. 1.12 Стационарные вероятности р_к для СМО типа М/М/1.

Теперь найдем наиболее интересные характеристики.

Важной характеристикой системы является средняя длина очереди. Зная вероятности каждого из возможных значений длины, найдем математическое ожидание:

.

График средней длины очереди заявок в системе в зависимости от значения коэффициента использования или нагрузки показан на рис. 1.13.

Найдем теперь дисперсию длины очереди: .

Для нахождения среднего значения времени пребывания в очереди воспользуемся формулой Литтла.

.

На рис. 1.14 приведен график зависимости среднего времени пребывания в очереди в зависимости от коэффициента использования (нагрузки).

Рассматривая полученные результаты, нетрудно видеть, что при увеличении коэффициента использования, как длина очереди, так и время пребывания в ней неограниченно возрастают при приближении ρ к единице. Такой вид зависимости от коэффициента использования характерен для почти всех СМО.

Наконец найдем вероятность того, что в очереди будет находиться не менее чем k заявок и того, что в очереди менее k заявок.

Итак, в ходе анализа простей шей системы М/М/1 нам удалось в аналитическом виде найти все практически интересные характеристики Q_oS системы.

1.3.2 Cистема с конечным накопителем: M/M/1:N

Рассмотрим СМО, для которой фиксировано максимальное число ожидающих заявок. Предположим, что в системе может находиться N заявок, включая находящуюся на обслуживании в сервере. Любое поступившее сверх этого числа требование получает отказ и немедленно покидает систему. В телефонии такие вызовы называют потерянными. Поступающие заявки образуют Пуассоновский поток, а обслуживание осуществляется одним сервером с показательным законом распределения времени обработки. Приспособим для описания такой системы модель процесса гибели-размножения.

Эта система эргодична и диаграмма интенсивностей переходов может быть изображена так как на рис. 1.15.

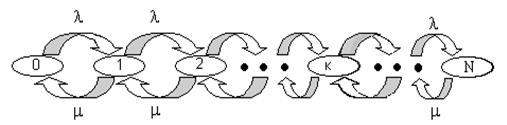
Рис. 1.15 Диаграмма интенсивностей переходов системы типа М/М/1:N.

Найдем распределение вероятностей в стационарном режиме непосредственно из общей формулы

Найдем теперь начальную вероятность, следуя общей формуле:

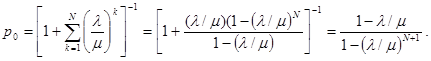
Таким образом, окончательная формула для стационарных вероятностей будет:

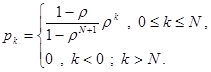
Проанализируем характеристики качества обслуживания (QoS) для такой системы. Важнейшей характеристикой будет являться вероятность блокировки – потери заявки. Очевидно, что это произойдет с вероятностью переполнения буфера, поэтому для расчета вероятности блокировки можно использовать формулу:

.

Например, для системы с коэффициентом использования 0.5 при размере буфера N =18 вероятность блокировки будет больше 10^-6, а при размере N =19, меньше этого значения. Следовательно, для получения вероятности блокировки такой величины необходимо предусмотреть размер буфера не менее 19.

Средняя длина очереди в буфере может быть найдена как:

.

Соответственно задержка может быть найдена на основе формулы Литтла

.

Определим пропускную способность системы как число заявок, обслуживаемых системой в одну секунду. Очевидно, что при вероятности блокировки P_B пропускная способность может быть найдена как чистая интенсивность поступлений, то есть:

.

С точки зрения выхода системы пропускная способность может быть определена иначе. Если система всегда была бы непуста, то ее производительность равнялась бы величине обратной среднему времени обслуживания, то есть μ. Однако, поскольку часть времени система может простаивать, вероятность того, что в ней нет ни одной заявки отлична от нуля, реальная производительность может быть выражена как:

.

Подставив выражения для вероятности простоя сервера для системы с бесконечным размером буфера, получим:

.

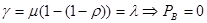Для системы с конечным буфером получаем:

.

В качестве реального примера рассмотрим концентратор сети с коммутацией пакетов, который обрабатывает пакеты со средней длиной 1200 бит. При скорости передачи в канале 2400 бит/с средняя пропускная способность его составит μ =2 пакета/с. Если полный входной поток имеет интенсивность λ =1 пакет/с, то ρ =0.5 и можно рассчитать, что при размере буфера N =9 пакетов в среднем по 1200 бит, вероятность блокировки составит 0.001. Для того, чтобы получить вероятность блокировки 0.000 001 нужно предусмотреть буфер длиной не менее 19 пакетов по 1200 бит, т.е. около 2850 байт.

1.3.3 Система с несколькими серверами: M/M/m

Рассмотрим сначала простой случай системы, содержащей два сервера, любой из которых доступен для поступающих на вход заявок. Системы с несколькими серверами такого типа называют полнодоступными. Очевидно, что по сравнению с односерверной системой производительность будет выше. Сразу отметим, что интерес будет представлять сравнение с односерверной системой интенсивность обслуживания в которой в среднем вдвое выше, то есть мы ответим на вопрос что эффективнее удвоение скорости обработки или распараллеливание обработки.

Система M/M/2 может быть представлена как процесс размножения-гибели с параметрами:

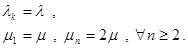
Найдем сначала распределение вероятностей в стационарном режиме:

Находя из условий нормировки вероятность простоя (нулевого состояния), находим

Найдем теперь основные характеристики качества обслуживания. Средняя длина очереди составит:

.

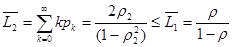Теперь найдем среднее время задержки в системе по формуле Литтла:

.

Таким образом, в системе с двумя серверами время задержки сокращается. Нетрудно убедиться, что производительность системы M/M/2 также выше, поскольку теперь средняя производительность будет определяться вероятностью занятости только одного сервера и незанятости обоих серверов:

.

Получилось, что производительность системы без блокировки также как и для системы с одним сервером совпадает с входной нагрузкой, тогда как максимальная производительность могла равняться 2μ.

Найдем теперь для сравнения характеристики качества обслуживания для односерверной системы с вдвое большей пропускной способностью сервера μ. Воспользуемся формулами для системы M/M/1.

На рис. 1.16 представлены нормированные графики среднего времени задержки в системе с одним и с двумя серверами одной и той же производительности и с одним серверов, работающим с вдвое большей скоростью. Как видно из сравнения, увеличение вдвое скорости работы сервера оказывается более эффективным, чем введение параллельного сервера той же производительности.

Рис. 1.16 Нормированные графики среднего времени задержки в системе с одним и с двумя серверами одной и той же производительности и с одним серверов, работающим с вдвое большей скоростью.

Рассмотрим теперь общий случай СМО с m серверами. Диаграмма интенсивностей переходов для такой системы представлена на рис. 1.17.

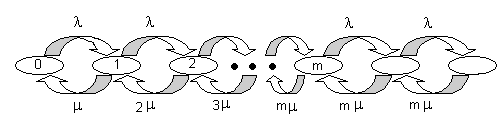
Рисунок 1.17. Диаграмма интенсивностей переходов для СМО типа M/M/m.

Интенсивности переходов могут быть определены следующим образом:

Используя основные общие соотношения для процессов гибели-размножения, получим:

Вероятность простоя определяется громоздкой формулой, которая может быть записана через общую входную нагрузку А и удельную нагрузку r на один сервер:

.

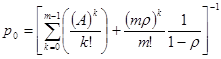Полученные здесь соотношения позволяют рассчитать все характеристики QoS, мы приведем только одну формулу, позволяющую найти вероятность того, что поступающее в систему заявка окажется в очереди. Эту формулу широко используют в телефонии: она определяет вероятность того, что поступающий на пучок из m линий вызов, не застанет ни одной свободной линии и будет поставлен в очередь на обслуживание. Эту формулу часто называют С-формулой Эрланга.

Модель СМО, описываемая С - формулой Эрланга называется также Lost Calls Delayed (LCD).

1.3.4 Система обслуживания с m серверами и с явными потерями: M/M/m:Loss

Предметом рассмотрения теперь будет система без образования очереди для заявок, поступивших в моменты, когда все m серверов были заняты. Такие заявки будут просто теряться. В телефонии это типичный случай коммутирования на конечном коммутационном поле. Опишем такую систему подходящим процессом типа гибели-размножения. Его параметры могут быть определены так

Такая система оказывается также эргодичной и диаграмма интенсивностей переходов, приведенная на рис. 1.18 позволяет найти распределение вероятностей:

Рис. 1.18 Диаграмма интенсивностей переходов для СМО типа M/M/m:Loss.

Основной характеристикой QoS для этой системы является средняя доля времени, когда все серверы оказываются занятыми. В этом случае говорят о том, что в системе наступила блокировка. Вероятность такой блокировки определяется по формуле, носящей в телефонии название В - формулы Эрланга или формулой потерь Эрланга

Эта формула играет столь большую роль в телефонии, что ее значения табулированы и существует масса таблиц, обратного расчета, то есть определения нагрузки, при которой обеспечивается заданная вероятность блокировки для заданного числа серверов. Такая таблица важна при расчетах многих сетей и систем массового обслуживания. Модель СМО, описываемая В - формулой Эрланга называется также Lost Calls Cleared (LCC).

1.3.5 Система обслуживания M/M/m:K/M конечное число источников нагрузки, m серверов и конечный накопитель.

Основной смысл изучения такой системы состоит в том, что входной поток в такой системе может рассматриваться как примитивный, то есть параметр потока зависит от числа требований, находящихся на обслуживании. Эта зависимость определяется таким образом, что из M источников пуассоновского потока с постоянным параметром λ получают отказ те требования, которые поступают в систему тогда, когда в ней уже имеются K заявок. Система описывается процессом типа гибели-размножения с диаграммой интенсивностей переходов на рис. 1.19.

Рис. 1.19 Диаграммой интенсивностей переходов для СМО типа M/M/m:K/М.

и параметрами интенсивностей:

Воспользовавшись формулам для стационарных вероятностей, получим:

Формула для вероятности простоя очень громоздка и здесь не приводится. Если считать, что K = m, то есть в системе только чистые потери (длина буфера совпадает с числом серверов), то распределение стационарных вероятностей может быть дано в виде так называемого распределения Энгсета:

Эта формула имеет следующую интерпретацию.

Некоторая система массового об­служивания, имеющая М входных линий, распределяет поступающие с них заявки на m серверов. Интен­сивность входного потока зависит от того, сколько серверов занято об­служиванием таким образом, что интенсивность входного потока ли­нейно убывает с числом занятых серверов: .

Максимальная нагрузка, поступающая на один вход, определяется как: .

Вероятность того, что при показательном законе распределения времени обслуживания в стационарном режиме будет занято k серверов, будет определяться как раз вышеприведенной формулой Энгсета. Систему такого типа можно назвать M/M/m:M. Полученное распределение также позволяет рассчитать вероятность того, что будут заняты все серверы. Для этого достаточно положить k = m. Как видно, она отличается от полученной ранее формулы потерь Эрланга. Это распределение также часто встречается на практике и задается функцией Энгсета:

.

На практике применима также модель Молина (Molina), которая также называется моделью потерянных вызовов (LCH – Lost Calls Held). Это математическая модель блокировки телефонного трафика, в которой блокированные обращения сохраняются в течение определенного времени задержки, хотя и не обслуживаются. Эта модель подобна модели, описываемой С – формулой Эрланга, с которой иногда и путается. Вероятность блокировки для N линий, создающих интенсивность А имеет вид:

.

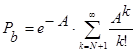1.3.6 Система типа M/M/m:m.

Как видно из обозначения, мы рассматриваем систему, имеющую одинаковое число входных линий и обслуживающих серверов, например выходных линий. Очевидно, что блокировка в такой системе невозможна. Диаграмма интенсивностей переходов состояний может быть представлена в виде совокупности несвязных m простейших подсистем с двумя состояниями – свободно/занято. (Рис. 1.20)

Рис. 1.20 Диаграмма интенсивностей переходов состояний для СМО типа M/M/m:m.

Вероятности того, что k подсистем находятся в состоянии «занято», описывается формулой Энгсета:

.

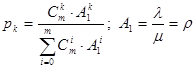Нетрудно видеть, что в этом случае в знаменателе записан бином Ньютона, и формула для вероятностей может быть существенно упрощена:

Полученное распределение вероятностей носит название биноминального или распределения Бернулли. Величина a определяет вероятность занятости сервера, а величина (1-a) – вероятность его простоя. Поскольку таких серверов m, то распределение вероятностей будет таким же, как для классической задачи о бросании m монет. Следует отметить также что

Дата добавления: 2015-08-02