А) Системы передачи с простым кодом

В системах передачи дискретных сообщений, передаваемых комбинациями простого кода, находят применение 5, 6, 7,8 - элементные коды.

В обычном режиме (без повторения) относительная скорость передачи данных равна:

R_о = 1,

а вероятность ошибок в знаке сообщения, поступающему к пользователю, равна:

Р_ош =Р(≥1, n).

Расчетные формулы для Р_ош имеют вид:

- для канала с независимыми ошибками: Р_ош = 1 – (1- р)ⁿ ≈ np;

- для канала с группирующимися ошибками: Р_ош = n^1-α p.

В этих формулах, как и ранее, приняты следующие обозначения:

- n – длина кодовой комбинации,

- р – вероятность ошибочного приема бита (битовая ошибка),

- α – показатель группирования ошибок по модели Л.П. Пуртова.

Таким образом, вероятность ошибки в знаке сообщения на выходе системы ПДС для различных каналов Р_ош > p, что не отвечает требованиям большинства пользователей.

Обеспечение требуемого уровня защиты от ошибок при использовании этих кодов в системах передачи данных возможно только в режиме многократного повторения. Каждая кодовая комбинация передается λ раз, где величина λ достаточно большое нечетное число. На принимающей станции выявление переданной источником комбинации производится по мажоритарному принципу, т.е. по большинству совпадения принятых значений. Возможны следующие методы анализа принятых комбинаций с целью принятия решения о переданной информации:

- решение по совпадению кодовых комбинаций (знаков сообщений),

- решение по совпадению элементов кодовых комбинаций.

Относительная скорость передачи в системах передачи данных простым кодом при λ- кратном повторении равна: R_о = 1/ λ.

Вероятность ошибки на выходе системы зависит от метода анализа принятых комбинаций.

В случае принятия решения по большинству совпадения повторяемых знаков сообщений ошибочный приём происходит в том случае, когда большинство из λ повторяемых знаков приняты с ошибками. Вероятность такого событияравна:

Р_ошз = .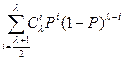

Здесь: - Р = Р(≥1, n) и вычисляется как было показано выше,

- С 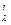- биномиальный коэффициент.

В системе с анализом элементов решение производится по каждому из n элементов λ повторяемых знаков. Оценка производится по большинству его принятых значений в последовательности из λ повторяемых знаков.

В данномслучае ошибочный приём происходит в том случае, когда большинство из λ повторяемых элементов на одинаковых позициях повторяемых знаков приняты с ошибками. Вероятность такого событияравна:

Р_ошэ = .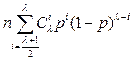

Здесь р – битовая ошибка.

Представляет интерес сравнить эти методы по эффективности защиты от ошибок. Для этого возьмем отношение Р_ошз к Р_ошэ:

Р_ошз / Р_ошэ = / ≈ .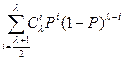

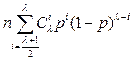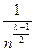При вычислении было принято Р = np и значение суммы определялось величиной первого слагаемого. Из результатов сравнения можно сделать вывод, что анализ по элементам при λ- кратном повторении передаваемой информации в n 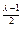раз дает меньшую ошибку, чем анализ по знакам. Таким образом, при мажоритарной обработке поэлементный анализ предпочтительнее, так как дает больше информации об ошибках.

Дата добавления: 2015-08-02