
Читайте также:
|
В обучении математике школьники должны овладеть не только знаниями, умениями и навыками, но и общими методами познания, общими способами учебной деятельности, одним из которых является моделирование.
Меделирование –это замена оригинала его моделью. Под моделью понимается заменитель оригинала, отражающий существенные и общие для некоторой группы объектов свойства и отношения и допускающий преобразование с целью получения новых знаний об оригинале.
В начале обучения нумерации ставят задачу: научить детей выделять главный признак некоторой группы предметов, абстрагируя при этом остальные, несущественные в данный момент. Особое внимание на занятиях, наряду с изучением содержания темы, предусмотренной учебной программой, уделяют формированию у детей мыслительных операций: анализа, синтеза, сравнения, обобщения. С этой целью сначала используют задания на выделение любых признаков одного предмета, затем нахождение сходных и различных признаков двух предметов, группы предметов. Основанием для выделения общего в начальном курсе математики служат признаки: цвет, размер, форма, наборы, …. Подобные задания способствуют формированию умения абстрагироваться от несущественного, выделять главное. Затем проводят работу на установление закономерности образования натурального ряда чисел.
С этой целью на наборном полотне выставляют полоски с кружками:
|
| ||||
|
| ||||
|
| ||||
|
| ||||
|
Детям предлагают задания: упорядочить полоски по какому – либо признаку. Для его выполнения они перемещают полоски с кружками до тех пор, пока на доске не появятся полоски с кружками, расположенными в порядке возрастания количества кружков. Отмечают, что вместо кружков могут быть поставлены другие предметы.
- Как узнать, сколько предметов на каждой полоске?
Учитель сообщает, что для обозначения числа предметов люди придумали особые знаки – цифры. На наборном полотне появляются цифры: 2,3,5,4,8,6,7,1,0,9. Всего 10 цифр. Возвращаясь к полоскам, дети соотносят каждой определенную цифру, обозначающую количество кружков на полоске. В результате такой работы появляется следующий результат:
| |||||
|
|
И т.д.
Обращают внимание на последовательность в расположении чисел и делают вывод: «В каждом следующем ряду кружков на один больше, значит каждое следующее число на единицу больше».
Описанные выше модели помогают уяснить состав числа. При помощи карандаша дети на модели делят кружки на две группы, устанавливая, сколько кружков всего.
Затем выполняют задания следующего плана:

 1. Вставь в «окошечко» нужное число:
1. Вставь в «окошечко» нужное число:
 8-1= 6 = +
8-1= 6 = +
 |  |
7 - = 6 9 = + 3 + 3.
2. Вставь в «окошечко» такие числа, чтобы равенства были верными:





+ = 5 + =
3. Как следует понимать запись?
7+1, +1.
Приобретенные детьми знания используют в дальнейшем при изучении нумерации чисел в пределах 100. На наборном полотне выставляют значки
|
|
|
чает цифру ноль. Это модели однозначных чисел и двузначных.
- Придумайте числа, которые бы соответствовали моделям:
|
|
|
|
|
Предлагают детям придумать самое маленькое, самое большое число, которое соответствует данным моделям.
При изучении нумерации чисел в пределах 1000 используют такие же модели чисел, как и в первых двух концентрах, но особое внимание уделяют преобразованию моделей.
Показывают модели чисел:
 |  |
|
Придумайте числа, которые бы соответствовали данным моделям. Работая с моделями, дети приходят к выводу, что все трехзначные числа можно разбить на 4 группы:
 |  |  |  |
Сравнивают модели полученных чисел: что в них общего, что различное? Разбивают модели на группы, имеющие какое-нибудь математическое сходство:
 |  |
- отсутствуют единицы какого –либо раз-
ряда.
 | |
 |
- единицы всех разрядов присутствуют.
|
|
|
|
Сравнивая модели чисел, находят признак, по которому можно сгруппировать трехзначные и двузначные числа:
 |  |
Р разрядные числа
 |  |  |  |
Числа, представленные данными моделями, можно заменить суммой разрядных слагаемых.
Используя модели чисел, составляют примеры:
 |
|  |
+ =
 | 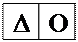 |  |
- =
 |
|  |
- =
 |  |  |
- =
 |  |  |
- =
Моделей примеров можно составить много. Свои ответы дети подтверждают конкретными примерами чисел, отмечают, что чисел можно назвать много. К одной и той же модели можно придумать множество числовых примеров.
|
|
|
|
|
|
При работе с классами чисел, полезно провести такую параллель:
|  | ||||
 |  |
 |  | ||||
 |  | ||||
 |  | ||||
 |  | ||||
 |  |
Так же идет работа по образованию вариантов чисел первого и второго классов. Идет работа следующего плана:
- постройте модель числа, имеющего 5 разрядов (придумать пример к этой модели),
- постройте модель шестизначного числа, в котором отсутствуют единицы 1 и 4 разрядов (привести пример числа по данной модели), ….
Параллельно с преобразованием моделей числа ведется работа по ее конкретизации. С этой целью предлагают такие задания:
1. Постройте модель шестизначного числа, конкретные примеры таких чисел подпишите под моделью.
2. Запишите число, состоящее из 867 единиц второго класса и 560 единиц первого класса.
3. Запишите число, в котором 2 единицы шестого разряда, 7 единиц четвертого разряда, 5 единиц первого разряда.
4. Запишите число, в котором всего 7907 десятков.
5. Запишите пятизначное число, в котором отсутствуют единицы первого класса.
6. Составьте модель шестизначного числа, в котором отсутствуют единицы 1,4,5 разрядов.
7.По данной модели запишите число и представьте его в виде суммы классных слагаемых, в виде суммы разрядных слагаемых:

Опыт показывает, что прием моделирования способствует развитию учащихся, так как работа с моделями помогает включить их в активную умственную деятельность. Изучение темы идет более быстрым темпом и обеспечивает осознанное усвоение материала, так как работа с моделями доступна учащимся младшего школьного возраста. Опора на модели облегчает самостоятельное выполнение заданий, выполнение заданий творческого характера. Использование моделей числа способствуют развитию логического мышления детей, заставляют их анализировать, сравнивать, обобщать, делать выводы.
Дата добавления: 2015-08-02; просмотров: 300 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задачи темы. | | | номеров поездам |