Эмпирическое распределение случайной величины

Интервалы значений	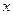Частота	Частость
0,00-0,05		0,02
0,05-0,10		0,12
0,10-0,15		0,24
0,15-0,20		0,40
0,20-0,25		0,22

Видно, что =100, = 1.

Эмпирическое распределение случайной величины может быть представлено в виде графика, который называют функцией распределения.

Если - случайная величина, а 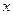- некоторое число, то при выполнении условия < 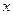событию соответствует вероятность < 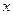), которая является функцией 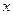: < 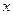) = 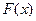. Функция 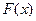называется интегральной функцией распределения. Она характеризует вероятность того, что случайная величина при испытаниях примет значение меньше произвольно изменяемого числа 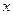при условии < <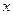+ (рис. 1).

Первая производная от неё – дифференциальная функция распределения или плотность вероятности . В зависимости от вида распределения случайной величины график её дифференциальной функции распределения может

иметь различную форму. Один из наиболее распространенных графиков - симметричная кривая Гаусса, которая характеризует закон нормального распределения (рис. 2).

	Рис. 2. График дифференциальной функции распределения

Распределения случайных величин имеют числовые характеристики, определяющие положение центра группирования случайной величины (меры положения) и её рассеивание около этого центра (меры рассеивания). Меры положения – это математическое ожидание и среднее арифметическое значение случайной величины. При выполнении лабораторных работ по химической кинетике чаще приходится рассчитывать среднее арифметическое значение случайной величины ()

,

где 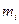- частости значений ; 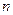- число отдельных значений . С учетом формулы (2) можно записать 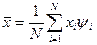или просто

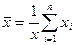. (3)

Математическое ожидание непрерывной случайной величины в диапазоне от - ∞ до + ∞ определяется по выражению , из которого видно, что необходимо задавать функцию распределения , что является непростой задачей.

Мерой рассеивания значений случайной величины относительно центра служит дисперсия случайной величины 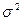. Её расчет зависит от - общего числа значений :

если ≤ 30, то вычисления следует выполнять по формуле

;

если > 30, то используется формула

.

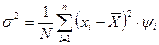Здесь 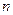- число значений . На практике обычно .

Величина называется средним квадратичным отклонением дисперсии.

Обычно времени для проведения большого количества опытов нет, поэтому возникает проблема совпадения характеристики распределения случайных величин, определенных по малому числу наблюдений, с теми же величинами, определенными по большому числу наблюдений, выполненных в тех же условиях. Для решения этой проблемы вводят понятия генеральной совокупности и выборки. Генеральная совокупность подразумевает все возможные в данных условиях наблюдения. Выборка – совокупность ограниченного числа наблюдений (при ≤ 30 выборки называют малыми, при > 30 – большими).

Выборочные характеристики рассматриваются как оценки соответствующих характеристик генеральной совокупности, однако сами выборочные характеристики случайной величины, в отличие от генеральных, являются случайными величинами.

Для того, чтобы выборочные характеристики достаточно правильно характеризовали параметры генеральной совокупности, они должны быть состоятельными, несмещенными и эффективными. Примером состоятельной и несмещенной оценки математического ожидания является среднее арифметическое значение 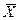, примером состоятельной, но смещенной оценки теоретической дисперсии 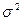является её выборочная оценка , которую называют среднеквадратичной ошибкой:

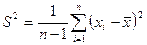. (4)

Выборочное среднеквадратичное отклонение , иначе называемое среднеквадратичной ошибкой среднего из измерений, определяется по формуле 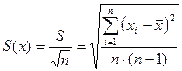или ,

где - единичные отклонения: .

Встречаются задачи, в которых закон распределения случайной величины отличается от нормального, но ошибка от принятия условия нормальности невелика и ею можно пренебречь. Поэтому во многих случаях при проведении химического эксперимента для ошибок измерений практически принимают нормальность распределения.

При малых выборках закон Гаусса неприменим. Если для случайной величины 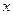математическое ожидание равно , то рассматриваемая величина подчиняется распределению Стьюдента, которое оценивается коэффициентом (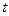): . Математическое ожидание в этом уравнении может быть заменено на среднеарифметическое значение, и тогда

. (5)

Значения коэффициента Стьюдента 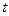зависят от числа степеней свободы 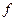выборочной дисперсии, определяемого по формуле , где - число параллельных опытов. Для различного числа степеней свободы кривые отличаются степенью «размытости» относительно точки максимума, проходящего через точку . При 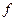< 20 степень «размытости» существенна, но уже при 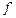> 20 кривая вполне удовлетворительно аппроксимируется дифференциальной функцией нормального распределения, а при совпадает с ней.

В табл. П. 4 показаны некоторые критические значения критерия Стьюдента при различных уровнях значимости. Обычно уровень значимости принимают в 5% (или 0,05), при этом уровень надежности составляет 95% (или 0,95).

По 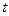- критерию Стьюдента определяют значимость коэффициентов регрессии 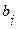( и т.д.) в уравнении (1). Для этого вычисляют значение - критерия каждого коэффициента по формуле (5) и, задав уровень значимости равным 0,05, находят критическое значение в табл. П. 4. Если расчетное значение окажется больше значения , найденного в таблице, то коэффициент признается значимым. В противоположном случае считается статистически незначимым и может быть отброшен без пересчета остальных коэффициентов.

При оценке погрешности результатов лабораторных работ рекомендуется такая последовательность расчетов:

1) находят среднеарифметическое значение по уравнению (3);

2) находят единичные отклонения , при этом проверяют, выполняется ли соотношение (в противном случае отбрасывают грубые ошибки и заново проводят расчет);

3) рассчитывают среднеквадратичную ошибку по формуле (4);

4) задавшись уровнем надежности в 0,95, выбирают в табл. П. 4 значение коэффициента 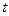в зависимости от числа измерений;

5) находят погрешность результата измерения по формуле ;

6) записывают окончательный результат в форме ;

7) находят относительную ошибку по формуле .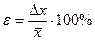

Для оценки отклонения какого-либо параметра процесса от среднего значения следует вычислять дисперсию воспроизводимости по данным параллельных опытов. Для проверки однородности дисперсий следует пользоваться критерием Кохрена (), который основан на законе распределения отношения максимальной дисперсии к сумме всех дисперсий:

. (6)

Критическое значение зависит от числа степеней свободы при оценке каждой из дисперсий (нужно, чтобы все дисперсии были рассчитаны по одному и тому же числу степеней свободы, т.е. число измерений во всех сериях опытов должно быть одинаково), а также от числа дисперсий и от уровня значимости (табл. П. 5).

Для проверки воспроизводимости измерений обычно задают уровень значимости в 5%, вычисляют () и находят табличное значение критерия Кохрена . Если расчетное значение , определенное по формуле (6), меньше найденного в таблице, то дисперсии однородны, и воспроизводимость результатов удовлетворительна. Если проверка дала отрицательный результат, то следует увеличить число параллельных опытов.

Проверку адекватности уравнения (1) проводят по критерию Фишера ()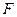

, (7)

где - оценка дисперсии адекватности, равная .

Формула (7) справедлива при равном числе параллельных опытов во всех сериях экспериментов.

Рассчитанное по ней значение критерия 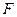сравнивают с табличным значением для определенного числа степеней свободы (табл. П. 6). Если расчетное значение критерия Фишера окажется меньше значения , определенного по таблице, то адекватность модели считается удовлетворительной.

Дата добавления: 2015-08-10