Реакции

Константа скорости реакции, определенная при одной температуре, не дает достаточно полной кинетической характеристики реакции. Скорость реакции существенно зависит от температуры.

Для приблизительной оценки влияния температуры на скорость реакции служит правило Вант-Гоффа, согласно которому повышение температуры на 10º увеличивает скорость химической реакции в 2÷4 раза

.

Точнее эту зависимость передает уравнение Аррениуса

(22)

или ,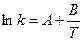

в котором 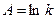и , где - предэкспоненциальный множитель; 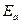- энергия активации; 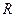- универсальная газовая постоянная. Уравнение (22) можно записать в виде

,

и тогда станет понятнее название . Предэкспоненциальный множитель определяется природой реакции и практически не зависит от температуры.

По теории активных соударений столкновения частиц может быть активным (эффективным) или неактивным. Химически реагировать, т.е. участвовать в активных соударениях, могут только молекулы, находящиеся в особом активном состоянии, в которое обычные молекулы могут переходить эндотермически. Концентрация таких активных молекул ничтожно мала, поэтому скорости обычных взаимодействий имеют конечные значения.

Для эффективности столкновений необходимо, чтобы они происходили между частицами, обладающими определенной энергией, избыточной по сравнению со средней. Энергия активации – минимальная энергия, которой должны обладать частицы, чтобы вступить в химическое взаимодействие. Энергия активации приближенно равна превышению энергии активированного комплекса над средним уровнем энергии исходных веществ. Энергия активации определяется природой реагирующих веществ и отвечает необходимости ослабления связей в тех молекулах, которые вступают во взаимодействие. Химический процесс сопровождается разрывом связей в исходных веществах и образованием новых химических связей в продуктах. Это становится возможным при переходе по пути реакции через энергетический барьер, характеризуемый энергией активации. Чем меньше энергетический барьер, тем легче осуществляется процесс, и тем больше его скорость.

Рассмотренные закономерности справедливы при сравнительно низких температурах (ниже температуры кипения) и в небольшом температурном интервале.

Энергия активации опытным путем находится по температурной зависимости констант скоростей реакции. Константы уравнения Аррениуса легко найти, располагая значениями константы скорости изучаемой реакции при двух температурах. Сделать это можно расчетным или графическим путем. Если по опытным данным построить график в осях , то он будет прямой линией, тангенс угла наклона которой позволит определить энергию активации. Нелинейность графика можно интерпретировать как непостоянство энергии активации реакции, что может иметь место в случае сложных реакций.

По отрезку на ординате, при условии , можно найти и вычислить непосредственное значение предэкспоненциального множителя.

Энергию активации химической реакции можно вычислить по уравнению

,

если известны константы скорости реакции при двух температурах, а далее по уравнению (22) определить .

Зная энергию активации реакции, можно вычислять константы скорости реакции при любых температурах.

Так как переход молекул в активном состоянии является обратимым процессом, то, рассматривая равновесие между активными и неактивными молекулами, можно получить дифференциальную форму уравнения Аррениуса . Термодинамическое её обоснование связано с уравнением изохоры или изобары Вант-Гоффа при соответствующих условиях. Например, уравнение температурной зависимости константы химического равновесия (): включает - стандартное изменение внутренней энергии. Следует отметить, что особой формы внутренней энергии, связанной с энергией активации, не существует. На рис. 6 показано распределение молекул по энергии, и видно соотношение энергии активации со средней энергией, которой обладает большая часть молекул в системе. С ростом температуры распределение молекул по энергиям меняется, кривая несколько смещается вправо, её верхняя часть становится низкой и пологой, а количество частиц с энергией равной или большей, чем энергия активации, резко возрастает, т.е. повышение температуры вызывает резкий прирост числа активных частиц и, следовательно, значительное ускорение реакции.

Рис. 6. Распределение молекул по кинетической энергии при различных температурах

Предэкспоненциальный множитель включает стерический фактор (от греч. sterios - пространственный), с помощью которого учитывают долю столкновений молекул с надлежащей ориентацией.

Столкнувшиеся молекулы могут не прореагировать, если они не имеют благоприятной ориентации в пространстве, т.е. не образуют конфигурации, способствующей разрыву одних и формированию других связей. Взаимодействию благоприятствует столкновение молекул в положениях, когда соприкасаются их реакционноспособные участки. Необходимость определенной конфигурации резко уменьшает число актов взаимодействия при столкновении активных молекул. Он гораздо меньше единицы и тем меньше, чем сложнее форма молекул реагентов.

Если энергия активации прямой реакции составляет величину , обратной - , то изобарный тепловой эффект реакции равен . Для эндотермической реакции > и > 0, для экзотермической, наоборот, < и < 0.

По теории активированного комплекса конечная конфигурация атомов продуктов достигается из начальной конфигурации исходных веществ при непрерывном изменении межатомных расстояний. При таком непрерывном изменении существует некоторая критическая конфигурация, соответствующая высшей точке наиболее выгодного пути реакции по поверхности потенциальной энергии. Именно эту конфигурацию называют активированным комплексом или переходным состоянием, когда исходных веществ уже нет, а продуктов ещё нет. Активированный комплекс можно рассматривать как обыкновенную молекулу с обычными термодинамическими свойствами при допущении, что движение вдоль координаты реакции приводит к его распаду на части с определенной скоростью (рис. 7).

Здесь – потенциальная энергия исходных веществ; – потенциальная энергия активного комплекса; – потенциальная энергия продуктов реакции; – разность между потенциальной энергией и потенциальной энергией активного комплекса в перевальной точке равна энергии активации, обладая которой молекулы исходных веществ и 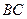в состоянии преодолеть потенциальный барьер и перейти в конечные продукты реакции и ; – энергия активации обратного процесса; – некоторый интервал вдоль пути реакции, включающий вершину потенциального барьера. Существующая в этом интервале конфигурация атомов, движущихся на энергетической диаграмме в сторону конечных продуктов, называется активным комплексом или переходным состоянием. 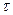Система проходит участок за некоторое время , называемым средним временем жизни активного комплекса; – изменение энтальпии в результате реакции равна разности между и .

Кривая на диаграмме представляет собой профиль пути реакции (рис. 7). Основное уравнение теории активированного комплекса имеет вид

, (23)

где - трансмиссионный коэффициент, для которого в настоящее время не существует теоретических путей расчета, но практически для большинства реакций, протекающих адиабатически, он равен единице. Кроме того, в уравнении (22) - постоянная Планка; - постоянная Больцмана; - константа химического равновесия между активированным комплексом и исходными веществами с учетом одномерного движения вдоль координаты реакции. Множитель , имеющий размерность обратного времени (с^-1), называется эффективной скоростью перехода активированных комплексов через энергетический барьер.

В рамках статистической термодинамики константу равновесия можно выразить через суммы по состояниям, и тогда уравнение (22) принимает вид

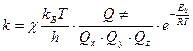, (24)

где - молекулярные суммы по состояниям, которые учитывают вклад каждого вида энергии – поступательной, вращательной, колебательной;

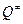имеет на одну колебательную степень свободы меньше обычной молекулы;

- истинная энергия активации, равная разности нулевых энергий активированного комплекса и исходных веществ (идентична энтальпии или опытной энергии активации при абсолютном нуле).

Уравнение (24) позволяет рассчитывать предэкспоненциальный множитель и константу скорости бимолекулярных реакций на основании сведений о размерах, геометрической конфигурации, основных частотах колебаний реагентов.

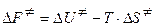По теории активированного комплекса к величине можно применять известные термодинамические соотношения: и , где 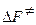- стандартная энергия активации Гельмгольца; - энтропия активации при стандартном состоянии; - внутренняя энергия активации. Тогда для реакции, протекающей при постоянном объеме, можно записать

. (25)

Множитель необходим для получения одинаковой размерности в обеих частях уравнения, его значение зависит от выбора стандартного состояния и молекулярности реакции, показывает изменение числа молекул при образовании активированного комплекса: = 1- 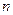( 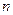- число вступающих в реакцию молекул).

При сравнении расчетных и опытных данных в соотношении (25) заменяют неопределяемую на опыте величину 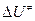на экспериментальное значение энергии активации по соотношению и получают

.

Можно заметить, что множитель перед равен предэкспоненциальному в уравнении Аррениуса; а отдельно энтропийный множитель 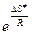по смыслу соответствует стерическому фактору, введенному теорией активных столкновений.

Если реакция протекает в газовой фазе, заменяют на 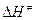, и это приводит к уравнению

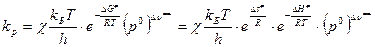. (26)

Из соображений, что , аналогично можно получить , где 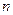- число молекул, участвующих в образовании активированного комплекса.

На практике константу скорости обычно выражают в единицах концентрации, поэтому с учетом соотношения между константами равновесия , формула (26) преображается

. (27)

Практически удобно использовать следующие обозначения: и , тогда получается простое выражение для расчета 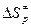- энтропии активации

.

Для бимолекулярных реакций 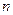= 2 и уравнение (27) принимает вид

.

Энтропию активации можно вычислить по уравнению

.

Дата добавления: 2015-08-10