Элементы теории вероятностей и математической статистики

Результаты химических экспериментов при установлении вида зависимости обычно выражаются в виде точечных оценок, для которых важен доверительный интервал. Результаты этих измерений носят статистический характер. Поэтому при обработке и анализе результатов исследований используется аппарат теории вероятности и математической статистики. Теория вероятности оперирует следующими понятиями:

Случайная величина – переменная величина, которая в результате испытания может принять то или иное значение.

Понятие вероятности используется для количественной оценки осуществления случайного события. Вероятность какого – либо события обозначают 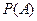. Она определяется из соотношения: , где - число случаев, благоприятствующих событию , 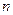- число всех возможных случаев. Вероятность достоверного события принимается равной единице, а вероятность невозможного – нулю. Вероятности возможных, но не достоверных событий характеризуются числами, лежащими в интервале от нуля до единицы.

Частота 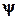появления события : в процессе испытаний случайное событие может произойти несколько раз, например 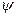раз. Относительная частость 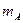определяется как отношение частоты события к общему числу испытаний ():

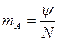. (2)

Если случайное событие имеет устойчивую частость в серии массовых испытаний, то это число называют статистической вероятностью события.

Случайные величины могут быть дискретными и непрерывными. Дискретные величины в результате испытаний принимают лишь конкретные фиксированные значения. Непрерывными случайными величинами называют величины, в результате испытания принимающие любые значения в границах определенного интервала.

Совокупность значений случайной величины, расположенных в возрастающем порядке с указанием вероятностей или частостей, называют распределением случайной величины.

На практике при изучении распределений непрерывных случайных величин делят диапазон их возможных значений на отдельные участки (интервалы). Подсчитывают общее число испытаний и частости появления события во всех интервалах. Для примера в табл. 1 приведен диапазон от 0,00 до 0,25.

Таблица 1

Дата добавления: 2015-08-10