Порядка реакии по экспериментальным данным

Кинетические расчеты сводятся к установлению порядка реакции и её константы скорости при данной температуре. Методы определения этих кинетических параметров подразделяются на дифференциальные и интегральные в зависимости от того, какая форма, дифференциальная или интегральная, основного кинетического уравнения используется в расчетах.

Дифференциальные методы:

расчетный метод. Используя данные эксперимента, по уравнению (11) рассчитывают средние значения скоростей процесса для нескольких промежутков времени и соответствующие им средние значения концентраций реагирующих веществ. Отношение каждой пары кинетических уравнений позволяет вычислить несколько значений 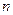, например, или , откуда 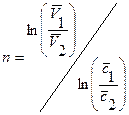. Окончательно порядок определяется как среднее арифметическое из всех рассчитанных 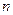. Зная порядок, по кинетическому уравнению можно рассчитать константу скорости реакции . Сделать это можно столько раз, сколько позволяют экспериментальные данные. Использовать при этом стоит уже усредненный порядок, а несколько величин констант скорости также следует усреднить.

С помощью этого метода можно определять частные порядки по каждому веществу, вступающему в реакцию. Сумма частных порядков определяет порядок реакции в целом.

графический метод. Предполагает логарифмирование основного кинетического уравнения (13) для линеаризации в виде (в этих расчетах можно использовать и десятичную форму логарифма). На рис. 5 показано, что в осях экспериментальные данные располагаются на прямой (при небольшом рассеянии точек, связанном с неизбежными ошибками при получении экспериментальных данных). Тангенс угла наклона этой прямой равен порядку реакции: (отрезки и берутся в масштабе соответствующих осей). Отрезок 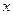, отсекаемый прямой на ординате при условии , равен , т.е. , откуда .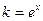

Интегральные методы:

расчетный метод или метод подстановки заключается в том, что в интегральные формы кинетического уравнения подставляют данные кинетического эксперимента. При этом находят, какое из уравнений дает постоянную величину константы скорости реакции. Например, при подстановке опытных данных в уравнение первого порядка 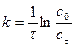получены следующие значения: 0,089; 0,077; 0,069; 0,052; 0,039, а при подстановке в уравнение второго порядка получены значения: 0,0070; 0,0066; 0,0068; 0,0071; 0,0066; 0,0067. Первые результаты характеризует монотонное снижение, вторые хорошо усредняются, поэтому рассматриваемая реакция протекает по второму порядку со средней константой 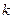= 0,0068 ().

графический метод: в табл. 2 представлены виды интегральных уравнений скорости в применении к реакциям нулевого, первого и второго порядков и показана возможность нахождения константы скорости. Линейность графика в соответствующих координатах указывает на порядок реакции, наклон графика, определяемый по тангенсу угла наклона, позволяет найти константу скорости реакции.

Таблица 2

Дата добавления: 2015-08-10