
Читайте также:
|
Абсолютные величины имеют размерность, т.е. имеют следующие единицы измерения:
1) натуральные (делятся на простые и сложные);
2) условно-натуральные;
3) стоимостные.
| Относительный показатель плана и реализации плана: |  
|
| Относительный показатель структуры: | 
|
| Название степенной средней | простая | взвешенная |
| Средняя гармоническая | 
| 
|
| Средняя геометрическая | 
| 
|
| Средняя арифметическая | 
| 
|
| Средняя квадратическая | 
| 
|
Свойство мажорантности степенных средних: 
Для исчисления средней в интервальном (непрерывном) ряду распределения, в качестве осредняемого индивидуального значения берут середины интервалов.
Мода – значение признака, наиболее часто встречаемое в исследуемой совокупности.
Медиана - значение признака, которое делит численность упорядоченного вариационного ряда на две равные части: одна часть имеет значения варьируемого признака меньшие, чем срединный вариант (медиана), другая – большие.
| Структурные средние в интервальномряду: | |
| Мода: | 
|
| Медиана: | 
|
67. Показатели вариации
| Название показателя | Формула | |
| Размах | 
| |
| простая | взвешенная | |
| Среднее линейное отклонение: | 
| 
|
| Дисперсия: | 
| 
|
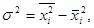 а для альтернативных признаков: а для альтернативных признаков: 
| ||
| Среднее квадратическое отклонение: | 
| |
| Показатели интенсивности вариации (относительные) | ||
| Коэффициент осцилляции: | 
| |
| Относительное линейное отклонение: | 
| |
| Коэффициент вариации: | 
|
Правило сложения дисперсий: 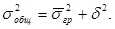
| Название дисперсии | Формула |
| Общая | 
|
| Межгрупповая | 
|
| Средняя из внутригрупповых | 
|
| Коэффициент детерминации: | 
|
| Эмпирическое корреляционное отношение | 
|
Дата добавления: 2015-08-10; просмотров: 110 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Сводка и группировка | | | Абсолютные и относительные характеристики динамического ряда |