Выборочное наблюдение

Выборочное наблюдение – вид статистического наблюдения, при котором обследованию подвергается не вся изучаемая совокупность, а лишь часть ее единиц, отобранных в определенном порядке. При этом вся исследуемая совокупность называется генеральной, а единицы, подлежащие наблюдению, составляют выборочную совокупность, или выборку.

Целью выборочного наблюдения является определение параметров генеральной совокупности (генеральной средней - 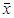и генеральной доли[1] - p) на основе параметров выборочной совокупности (выборочной средней - 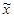и выборочной доли - ).

Разница между генеральными и выборочными параметрами называется ошибкой выборки или ошибкой репрезентативности.

Специальные этапы выборочного наблюдения:

а) определение необходимого объема выборки и способа отбора;

б) проведение отбора;

в) обобщение данных наблюдения и расчет выборочных характери­стик;

г) расчет ошибок выборки;

д) распространение выборочных характеристик на генеральную сово­купность.

Различают два вида отбора единиц из генеральной совокупности - повторный и бесповторный.

Оба способа могут быть реализованы в следующих основных видах выборки: собственно случайная (в соответствии с правилами случайного отбора); механическая (например, по нейтральным спискам единиц отбора); типическая (районированная – обеспечивает представительство в выборке типических групп генеральной совокупности для увеличения точности); серийная (отбирают­ся целые серии или гнезда и в них обследуются все единицы); комбиниро­ванная; многоступенчатая (выборочная совокупность формируется по­степенно, по ступеням отбора); многофазная (совокупность формируется из ряда последовательных подвыборок); взаимопроникающая (это две или более независимые выборки из одной и той же совокупности, образован­ные одним способом и видом).

Необходимая численность выборки определяется по особым форму­лам, выведенным из формул предельных ошибок выборки с учетом спосо­бов и видов отбора. Элементами этих формул являются: N (объем генеральной со­вокупности), (дисперсия признака генеральной совокупности), п (объем выборочной совокупности), Δ (предельная ошибка выборки), t (коэффициент доверия)[2].Перемен­ными величинами выступают только последние три, но две из них задают­ся исследователем. Величина t в экономических расчетах обычно берется в пределах от 2 до 3, что соответствует вероятно­сти от 0,954 до 0,997. Величина Δ, как пра­вило, задается в пределах до 10% предполагаемого среднего уровня при­знака. Сигму () можно условно принять за (если известен раз­мах вариации признака R по изучаемому явлению) или за или (если ге­неральная совокупность близка к нормальной).

объем выборки для собственно случайного повторного отбора
объем выборки для бесповторного отбора

Под средней ошибкой понимают такое расхождение между средними выборочной и генеральной совокупностями (), которое не превышает ±σ. При случайном и механическом отборах средняя ошибка выборки для средней величины определяется следующим образом:

при повторном отборе
при бесповторном отборе

Предельной ошибкой ( ,где t – коэффициент доверия) принято считать максимально возможное расхождение этих средних, т.е. максимум ошибки при заданной вероятности ее появления.

По величине предельной ошибки можно вычислять предельные значения характери­стик генеральной совокупности при заданной вероятности, а именно:

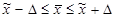
Дата добавления: 2015-08-10