Читайте также:
|
Агрегатный индекс – это отношение суммы отчетных значений индексируемого признака, взвешенных на соответствующих значениях, к сумме значений индексируемого признака.
Рассмотрим методологию построения сводных индексов в агрегатной форме. Построение и исчисление сводных индексов сложных (соизмеримых объемных показателей) сводится к обычным относительным величинам – индексам в широком их смысле.
Поясним это на формулах индексной символики. Предварительно показатель, характеризующий уровень сложного явления, образующегося как произведение его отдельных факторов, условно назовем сложным или соизмеримым объемным показателем.
Пусть сложный показатель (например, стоимость произведенной продукции) представляет собой произведение двух показателей – факторов:
качественного показателя – Х ( в нашем примере р - цены единицы продукции);
объемного несоизмеримого показателя – У (Q - количества произведенной продукции отдельных видов в натуральном выражении).
Уровень сложного показателя обозначим:
в отчетном периоде -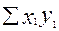 
в базисном периоде - 
.
Тогда формула сводного индекса в агрегатной форме: 
, что означает относительное изменение сложного показателя в отчетном периоде по сравнению с базисным.
При этом разность между числителем и знаменателем данного индекса характеризует изменение сложного показателя в абсолютном выражении: 
В нашем примере:
- 
- стоимость всей продукции в базисном периоде;
- 
- стоимость всей продукции в отчетном периоде.
Сопоставив эти два показателя, получим индекс стоимости всей продукции: 
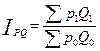, который показывает относительное изменение стоимости всей продукции, как за счет изменения цен, так и за счет изменения объема по отдельным видам продукции.
Соответственно, разность между числителем и знаменателем данного индекса представляет абсолютное изменение стоимости произведенной продукции в отчетном периоде по сравнению с базисным: 
Несколько иначе решается вопрос при построении сводных индексов, характеризующих динамику непосредственно несоизмеримых, разнородных явлений, когда требуется выразить в общем виде одним показателем изменения всех элементов сложного явления.
Сводные индексы несоизмеримых объемных показателей и сводные индексы качественных показателей являются особыми относительными величинами, индексами в собственном смысле слова, индексами в узком понимании. Построение этих сводных индексов требует использования специфических особенностей индексного метода:
1. Изменение изучаемого явления должно рассматриваться не изолированно, а во взаимосвязи с другим явлением. При этом показатель – сомножитель, связанный с индексируемым показателем, при построении собственно индексов играет роль статистических весов;
2. Устранение влияния изменения весов осуществляется путем их фиксирования в числителе и знаменателе индекса на одном и том же уровне.
При построении агрегатных индексов объемных показателей возникает проблема соизмерения отдельных элементов изучаемого сложного явления (например, различные виды продукции или товаров в натурально-вещественной форм несоизмеримы, поскольку обладают различными потребительскими свойствами, для их производства требуются разные затраты труда). Неоднородную продукцию, не допускающую непосредственного суммирования, можно с помощью определенных соизмерителей выразить в одинаковых единицах измерения и, определив в них общий объем продукции в отчетном и базисном периодах, найти отношение этих общих объемов).
Соизмеримость достигается умножением индексируемого объемного показателя на качественный показатель (например, цену, себестоимость или трудоемкость единицы продукции). При этом внешней отличительной особенностью агрегатного индекса является то, что в числителе и в знаменателе меняется индексируемая величина, значения же другой, являющейся соизмерителем, остаются неизменными
Выбор коэффициента соизмерения в каждом конкретном случае зависит от цели исследователя. При этом возможны разные варианты решения:
1 вариант. Если принять за коэффициент соизмерения качественный показатель базисного периода (в нашем примере – цены базисного периода), то индекс будет иметь следующий вид:
или в нашем примере: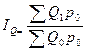 
Это вариант построения агрегатного индекса Э.Ласпейреса (предложен в 1864 году). В данном варианте индекса количественных показателей значения соизмерителей (качественных показателей) принимаются на уровне базисного периодп.
Например, при проведении экономико-статистического анализа при исчислении системы индексов за последовательные периоды времени обычно применяют во всех индексах величину качественного показателя-соизмерителя на уровне одного и того же периода.
2 вариант. Если использоватьза коэффициент соизмерения качественный показатель отчетного периода, тогда индекс объемного несоизмеримого показателя примет вид:
или в нашем примере: 
Это вариант построения агрегатного индекса Г.Пааше (предложен в 1874году).
При построении агрегатных индексов качественных показателей возникает необходимость взвешивания, разрешающаяся умножением определенных уровней качественных показателей на соответствующие значения связанных с ними объемных показателей.
Например, для определения общего изменения уровня цен на продукцию пищекомбината, включающую различные виды, нужно рассчитать агрегатный индекс цен. при невозможности непосредственного суммирования уровня цен 1 кг печенья и 1 кг конфет и т.д.(ввиду отсутствия экономического содержания итогового показателя).
Невозможность суммирования уровней преодолевается путем взвешивания индексируемого качественного показателя (в примере -цену каждого вида продукции) на соответствующий объемный показатель (в примере - на количество произведенных единиц продукции). При этом показатель веса - объемный показатель- фиксируется в числителе и знаменателе индекса на уровне одного и того же периода. При этом возможны разные варианты решения:
1 вариант. Если принять качестве веса объемный показатель отчетного периода (в нашем примере –объем продукции отчетного периода), то сводный индекс качественного показателя будет иметь следующий вид(формула Пааше): 
, а в нашем примере: 
2 вариант. Если использоватьв качествевеса объемный показатель базисного периода, тогда получим сводный индекс качественного показателя по формуле Ласпейреса:
или формула агрегатного индекса цен в нашем примере: 
В экономической практике используются формулы индексов цен и Ласпейреса и Пааше, хотя они дают разные результаты (По значению индекс Ласпейреса больше индекса Пааше). Каждый из этих индексов имеет свои особенности, имеющие свое предпочтение в конкретных случаях применения.
Так, индекс цен Ласпейреса удобен:
- для оперативной (месячной, квартальной) информации об изменении цен на определенный фиксированный набор товаров, когда пересчет каждый раз на текущий набор (количество) товаров сопряжен с большими затратами труда и времени (по формуле Ласпейреса рассчитывают индекс потребительских цен).
- ввиду возможности перехода от ряда индексов с переменной базой сравнения к ряду индексов с постоянной базой сравнения и обратно.
Формуле Пааше (продукция фиксируется на уровне текущего периода) отдается предпочтение в случае:
- когда индекс цен рассматривается в системе с индексом стоимости и индексом объема.
- если, вычитая из числителя знаменатель, можно определить сумму потерь (или прибыли) за счет изменения цен на продукцию отчетного (текущего) периода.
Приведенные варианты исчисления индексов отражают практику отечественной статистики. Во многих странах индексы физического объема и цен также исчисляются аналогичным образом. В международной статистике для расчетов рекомендуются и другие формы индексов.
Например, американским экономистом И.Фишером предложено вместо формул индексов Ласпейреса и Пааше использовать среднюю геометрическую, то есть корень квадратный из их произведения. Этот индекс получил название «идеального», так как в этом варианте расчета не отдается предпочтение ни показателю- соизмерителю базисного периода, ни соизмерителю отчетного периода.
При принятии решения при выборе метода расчета индексов следует руководствоваться:
- целями исследователя;
- возможностями получения статистической информации;
- потребностями удешевления затрат на ее получение.
Приведенные выше индексы в агрегатной форме используются для характеристики изменения уровня сложных экономических показателей. Но можно их использовать и в аналитических целях: для оценки влияния на результативный показатель изменения факторов, его формирующих.
Предпосылкой для применения индексного метода в экономическом анализе является возможность представления результативного показателя произведением двух или более составляющих его величину показателей (факторов) или суммы таких произведений. При этом следует учитывать, что если сложный показатель-результат является произведением двух и более показателей-сомножителей (факторов), то и индекс сложного (результативного) показателя является произведением индексов показателей сомножителей (факторов).
При оценке роли отдельных факторов на изменение результативного показателя задача состоит в том, чтобы рассчитать изменение сложного показателя при изменении величины только одного фактора, а величина другого показателя-фактора должна быть сохранена на определенном постоянном уровне.
В основе приема аналитических индексных расчетов лежит принцип элиминирования изменений величины всех факторов, кроме изучаемого. При построении индексов, оценивающих влияние отдельных факторов на изменение сложного показателя, необходимо иметь в виду, что общий результат изменения этого показателя представляет собой сумму изменения за счет влияния всех исследуемых факторов, формирующих этот показатель.
При использовании индексного метода для факторного анализа необходимо выполнение следующих условий:
1) при расчете индексов объемных несопоставимых показателей соизмерители принимаются на уровне базисного (более раннего) периода (то есть расчет ведется по формуле Ласпейреса):
или в нашем примере:
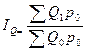
2) при расчете индексов качественных показателей веса в числителе и знаменателе фиксируются на уровне текущего (отчетного, более позднего) периода (то есть используется формула Пааше): , а в нашем примере:
Рассмотрим факторный анализ экономических показателей с помощью индексного метода.
Дата добавления: 2015-08-02; просмотров: 225 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Объемные показатели Качественные показатели | | | Задача 1. |