Читайте также:
|
Рассмотренные выше индексы определяют средний размер изменения индексируемого показателя (в агрегатной форме) для совокупности несоизмеримых, разнородных элементов.
При изучении динамики качественных показателей для однородной совокупности определяется изменение средней величины индексируемого показателя.
Например, по совокупности заводов, выпускающих одну и ту же продукцию, но с разным уровнем себестоимости, требуется показать изменение средней себестоимости данного вида продукции.
В общем виде динамику средних показателей можно выразить отношением 
, которое является относительным показателем динамики и называется индексом средних величин.
Относительная величина, характеризующая динамику двух средних показателей для однородной совокупности, представляет собой индекс переменного состава. Поскольку средние величины при этом рассчитываются как взвешенные, то индекс переменного состава для любого качественного показателя можно записать в виде: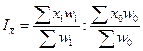 
где Х – индексируемые величины (качественный показатель),
W – веса индекса.
Свое название эти индексы получили потому, что средние величины, динамику которых они отражают, могут меняться не только за счет изменения индексируемого показателя у отдельных объектов (частей целого), но и за счет изменения удельного веса (доли) этих частей в общей совокупности (изменение состава структуры). Соответственно, формула индекса переменного состава видоизменится: 
где dw – удельный вес (доля) показателя веса (объемного показателя) у
отдельных частей, объектов общей совокупности в общем
объеме совокупности.
В нашем примере индекс переменного состава отражает изменение средней себестоимости определенного вида продукции по совокупности предприятий за отчетный период (или по сравнению с планом) за счет изменения себестоимости единицы продукции данного вида на каждом предприятии и за счет изменения доли объема продукции, производимой на каждом заводе, в общем объеме продукции, выпускаемой совокупностью всех предприятий.
Чтобы исключить влияние изменения структуры совокупности на динамику средних величин, средние показатели для двух периодов рассчитывают по одной и той же фиксированной структуре (фиксирование осуществляется на уровне отчетного периода). Индекс, характеризующий динамику средних величин при постоянной структуре совокупности, носит название индекса постоянного, фиксированного состава: 
В нашем примере индекс фиксированного состава представляет собой изменение средней себестоимости единицы данного вида продукции по совокупности предприятий за счет изменения себестоимости единицы данного вида продукции на каждом предприятии.
Если в индексе фиксированного состава 
произвести сокращение на ∑Q1, то формула принимает вид известного агрегатного индекса качественного показателя: 
Таким образом, индекс фиксированного состава осредняет изменение индексируемого качественного показателя, без учета изменения структуры совокупности.
Влияние структурного фактора на динамику среднего показателя устанавливается посредством индекса структурных сдвигов: 
Индекс структурных сдвигов характеризует относительное изменение средней величины качественного показателя в однородной совокупности за счет происшедших в ней за отчетный период структурных сдвигов. Например, индекс средней себестоимости (структурных сдвигов) показывает изменение средней себестоимости единицы определенного вида продукции по совокупности предприятий за счет изменения доли объема продукции данного вида, производимой на каждом предприятии в общем объеме продукции, выпускаемой по совокупности заводов.
По следующим данным о продаже моркови на двух колхозных рынках за 2 месяца вычислите: 1) индекс переменного состава: 2) индекс фиксированного состава: 3) индекс структуры.
| Номер рынка | Май | Июнь | ||
| цена за кг, коп. | продано, кг | цена за кг, коп | продано, кг | |
Приведем формулу сводного индекса качественного показателя в агрегатной форме:
Формула индекса характеризует относительное изменение сложного показателя (явления) за счет изменения уровня качественного показателя у отдельных элементов совокупности. Разность значений числителя и знаменателя показывает абсолютное изменение уровня сложного показателя при изменении уровня качественного показателя у отдельных единиц совокупности: 
Например, разность между числителем и знаменателем соответствующего индекса цены представляет абсолютную экономию или перерасход населения за счет изменения цен по отдельным видам реализованной продукции.
Рассмотренные выше индексы определяют средний размер изменения индексируемого показателя (в агрегатной форме) для совокупности несоизмеримых, разнородных элементов.
При изучении динамики качественных показателей для однородной совокупности определяется изменение средней величины индексируемого показателя.
Например, по совокупности заводов, выпускающих одну и ту же продукцию, но с разным уровнем себестоимости, требуется показать изменение средней себестоимости данного вида продукции.
В общем виде динамику средних показателей можно выразить отношением ________, которое является относительным показателем динамики и называется индексом средних величин.
Относительная величина, характеризующая динамику двух средних показателей для однородной совокупности, представляет собой индекс переменного состава. Поскольку средние величины при этом рассчитываются как взвешенные, то индекс переменного состава для любого качественного показателя можно записать в виде:
_________________________________________________________.
где Х – индексируемые величины (качественный показатель),
W – веса индекса.
Свое название эти индексы получили потому, что средние величины, динамику которых они отражают, могут меняться не только за счет изменения индексируемого показателя у отдельных объектов (частей целого), но и за счет изменения удельного веса (доли) этих частей в общей совокупности (изменение состава структуры). Соответственно, формула индекса переменного состава видоизменится: _______________________
где dw – удельный вес (доля) показателя веса (объемного показателя) у
отдельных частей, объектов общей совокупности в общем
объеме совокупности.
В нашем примере индекс переменного состава отражает изменение средней себестоимости определенного вида продукции по совокупности предприятий за отчетный период (или по сравнению с планом) за счет изменения себестоимости единицы продукции данного вида на каждом предприятии и за счет изменения доли объема продукции, производимой на каждом заводе, в общем объеме продукции, выпускаемой совокупностью всех предприятий.
Чтобы исключить влияние изменения структуры совокупности на динамику средних величин, средние показатели для двух периодов рассчитывают по одной и той же фиксированной структуре (фиксирование осуществляется на уровне отчетного периода). Индекс, характеризующий динамику средних величин при постоянной структуре совокупности, носит название индекса постоянного, фиксированного состава: ____________________________________.
В нашем примере индекс фиксированного состава представляет собой изменение средней себестоимости единицы данного вида продукции по совокупности предприятий за счет изменения себестоимости единицы данного вида продукции на каждом предприятии.
Если в индексе фиксированного состава ______________________ произвести сокращение на _________, то формула принимает вид известного агрегатного индекса качественного показателя: ________________________________________________.
Таким образом, индекс фиксированного состава осредняет изменение индексируемого качественного показателя, без учета изменения структуры совокупности.
Влияние структурного фактора на динамику среднего показателя устанавливается посредством индекса структурных сдвигов:
____________________________________________________.
Индекс структурных сдвигов характеризует относительное изменение средней величины качественного показателя в однородной совокупности за счет происшедших в ней за отчетный период структурных сдвигов. Например, индекс средней себестоимости (структурных сдвигов) показывает изменение средней себестоимости единицы определенного вида продукции по совокупности предприятий за счет изменения доли объема продукции данного вида, производимой на каждом предприятии в общем объеме продукции, выпускаемой по совокупности заводов.
Задачи и упражнения по общей теории статистики
Задача 1. Имеются следующие данные по магазинам одного города:
| Наименование товара | Продано, шт. | Оборот, тыс. руб. | ||
| апрель | май | апрель | Май | |
| А | 0,73 | 0,56 | ||
| Б | 5,60 | 4,30 | ||
| В | 14,49 | 14,77 |
Выясните, как изменилось в мае по сравнению с апрелем количество проданных товаров в целом, их товарооборот и определите среднюю величину изменения цен. Чему равна экономия или дополнительные затраты покупателей, вызванные изменениями цен по каждому товару и по всем товарам вместе?
Задача 2. По следующим данным о продаже моркови на двух колхозных рынках за 2 месяца вычислите: 1) индекс переменного состава: 2) индекс фиксированного состава: 3) индекс структуры.
| Номер рынка | Май | Июнь | ||
| цена за кг, коп. | продано, кг | цена за кг, коп | продано, кг | |
Задача 3. Определите среднее снижение себестоимости во II квартале по сравнению с себестоимостью I квартала по обоим видам продукции:
| Вид продукции | Общие затраты на производство, тыс. руб. | Снижение себестоимости единицы продукции по II квартале по сравнению с I кварталом, % | |
| I квартал | II квартал | ||
| Сумки дамские | |||
| Портфели |
Вопрос 1. Укажите, какой из индексов является общим индексом цен:
Вопрос 2. Укажите, какой из индексов является общим индексом товарооборота:
Вопрос 3. Укажите, какой из индексов является общим индексом физического объема товарооборота:
Дата добавления: 2015-08-02; просмотров: 154 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Средние из индивидуальных индексов | | | Сущность и значение индексного метода |