
Читайте также:
|
Алгебра событий. Классификация событий
Исходные понятия, определения
| 1.1. Записать определения следующих понятий: | ||||||||||||||||||||||||||||||||||||||||||
| Испытание (опыт) | - это наблюдение какого-либо явления при соблюдении определенного комплекса условий, который должен каждый раз строго выполняться при повторении данного испытания | |||||||||||||||||||||||||||||||||||||||||
| Элементарный исход | - это любой простейший (т.е. неделимый в рамках данного опыта) исход испытания | |||||||||||||||||||||||||||||||||||||||||
Пространство элементарных исходов ( ) )
| ||||||||||||||||||||||||||||||||||||||||||
Событие ( ) )
| ||||||||||||||||||||||||||||||||||||||||||
| 1.2. Описать пространство элементарных исходов. | ||||||||||||||||||||||||||||||||||||||||||
а) Опыт: по каналу связи последовательно передано три знака.
Решение.
Используем цифры 0, 1 для обозначения событий: 0 – знак искажен, 1 – знак принят. Тогда пространство элементарных событий запишется в виде  и имеет размерность восемь. и имеет размерность восемь.
| б) Опыт: на поверхность стола бросается монета.
Решение.
Результатом эксперимента будем считать координату центра монеты и величину угла поворота монеты.
Тогда пространство элементарных исходов – множество пар  , где , где 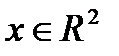 – точка стола и – точка стола и  – угол поворота. Число элементарных исходов такого эксперимента несчетно. – угол поворота. Число элементарных исходов такого эксперимента несчетно.
| |||||||||||||||||||||||||||||||||||||||||
| 1.3. Из приведенных примеров выделить следующие понятия: | ||||||||||||||||||||||||||||||||||||||||||
| Пример Понятие | 1) Монета подбрасывается до тех пор, пока не выпадет герб. | 2) При бросании игрального кубика выпало четное число очков. | 3) За экзамен студент получил положительную оценку. | |||||||||||||||||||||||||||||||||||||||
| Испытание (опыт) | Подбрасывание монеты | |||||||||||||||||||||||||||||||||||||||||
Пространство элементарных исходов ( ) )
| 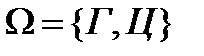
 герб, герб, 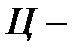 цифра цифра
| |||||||||||||||||||||||||||||||||||||||||
Событие ( ) )
| 
| |||||||||||||||||||||||||||||||||||||||||
| 1.4. Установите соответствие между понятием и его определением: | ||||||||||||||||||||||||||||||||||||||||||
| Список понятий: 1) достоверное событие; 2) невозможное событие; 3) равновозможные события; 4) полная группа событий; 5) случайное событие; 6) элементарное событие; 7) совместные события; 8) несовместные события; 9) зависимые события; 10) независимые события; 11) событие, противоположное данному. | ||||||||||||||||||||||||||||||||||||||||||
| а) | Равновозможные события | - это события, если условия их появления в опыте одинаковы и нет основания считать какое-либо из них более возможным, чем другое. | ||||||||||||||||||||||||||||||||||||||||
| б) | - это событие, которое при повторении опыта иногда происходит, а иногда нет. | |||||||||||||||||||||||||||||||||||||||||
| в) | Зависимые события | - это такие события, если наступление одного из них влияет на вероятность появления других. | ||||||||||||||||||||||||||||||||||||||||
| г) | Элементарное событие | - это событие, состоящее из одного элемента, его нельзя выразить через более простое. | ||||||||||||||||||||||||||||||||||||||||
| д) | - это такие события, когда наступление одного из событий сопровождается наступлением других в одном и том же испытании. | |||||||||||||||||||||||||||||||||||||||||
| е) | - это событие, которое не может появиться при испытании. | |||||||||||||||||||||||||||||||||||||||||
| ж) | - это событие, наступающее всякий раз, когда не появляется данное событие. | |||||||||||||||||||||||||||||||||||||||||
| з) | Несовместные события | - это события, когда появление одного из событий исключает появление другого. | ||||||||||||||||||||||||||||||||||||||||
| и) | - это событие, которое наступит при каждом испытании. | |||||||||||||||||||||||||||||||||||||||||
| к) | - это события, если наступление одного из них не влияет на вероятность появления других. | |||||||||||||||||||||||||||||||||||||||||
| л) | Полная группа событий | - это достоверное событие, которое образуют несколько попарно несовместных событий, то есть если в результате опыта обязательно произойдет одно и только одно из них. | ||||||||||||||||||||||||||||||||||||||||
| 1.5. Из изображенных на рисунке 1указать события: | ||||||||||||||||||||||||||||||||||||||||||
Дополнить ответ
1) совместные события:
2) несовместные события: | ||||||||||||||||||||||||||||||||||||||||||
| 1.6. Для указанного опыта выбрать указанные события(дополнить ответ) | ||||||||||||||||||||||||||||||||||||||||||
Опыт: брошены два игральных кубика.
События:
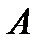 - сумма выпавших очков равна 8; - сумма выпавших очков равна 8;
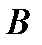 - произведение выпавших очков не больше 36; - произведение выпавших очков не больше 36;
 - на первом кубике выпавшая цифра четная; - на первом кубике выпавшая цифра четная;
 - хотя бы одна из выпавших цифр нечетная; - хотя бы одна из выпавших цифр нечетная;
 - сумма выпавших очков равна 50; - сумма выпавших очков равна 50;
 - сумма выпавших очков не больше 12; - сумма выпавших очков не больше 12;
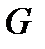 - произведение выпавших очков равно 1; - произведение выпавших очков равно 1;
 - на первом кубике выпавшая цифра нечетная. - на первом кубике выпавшая цифра нечетная.
 - на обоих кубиках четные цифры. - на обоих кубиках четные цифры.
| Достоверные события | 
| ||||||||||||||||||||||||||||||||||||||||
| Невозможные события | ||||||||||||||||||||||||||||||||||||||||||
| Противоположные события | 
| |||||||||||||||||||||||||||||||||||||||||
| Несовместные события | 
| |||||||||||||||||||||||||||||||||||||||||
| 1.7. Привести пример опыта так, чтобы событие – «Мисс МГТУ - брюнетка» являлось | ||||||||||||||||||||||||||||||||||||||||||
| а) достоверным | б) невозможным | в) случайным | ||||||||||||||||||||||||||||||||||||||||
| 1.8. Назвать противоположные события для следующих событий: | ||||||||||||||||||||||||||||||||||||||||||
а)  - выигрыш в лотерею. - выигрыш в лотерею.
| б)  - выигрыш в футбольном матче. - выигрыш в футбольном матче.
| |||||||||||||||||||||||||||||||||||||||||
| 1.9. Указать какие события из приведенных опытов являются равновозможными | ||||||||||||||||||||||||||||||||||||||||||
а) Опыт: выстрел по мишени.
События:  – попадание; – попадание;  – промах.
б) Опыт: на калькуляторе случайно набирается двузначное число.
События: – промах.
б) Опыт: на калькуляторе случайно набирается двузначное число.
События:  – появление четного числа; – появление четного числа;  – появление нечетного числа.
События: – появление нечетного числа.
События: 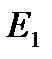 – появление простого числа; – появление простого числа; 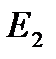 – появление составного числа.
в) Опыт: выбирается шар из урны, в которой 5 синих и 7 красных шаров;
все шары пронумерованы.
События: – появление составного числа.
в) Опыт: выбирается шар из урны, в которой 5 синих и 7 красных шаров;
все шары пронумерованы.
События:  – появление синего шара; – появление синего шара;  – появление красного шара;
События: – появление красного шара;
События: 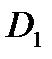 – появление шара с номером 1; – появление шара с номером 1;  – появление шара с номером 9. – появление шара с номером 9.
| ||||||||||||||||||||||||||||||||||||||||||
| 1.10. Укажите, какие события образуют полную группу событий в следующих опытах: | ||||||||||||||||||||||||||||||||||||||||||
а) Опыт – выбор наудачу двух целых чисел.
События:  - произведение чисел положительно, - произведение чисел положительно,  - произведение чисел отрицательно, - произведение чисел отрицательно,  - произведение чисел равно 0.
б) Опыт – сдача типовых расчетов на проверку.
События: - произведение чисел равно 0.
б) Опыт – сдача типовых расчетов на проверку.
События:  - один сдан, - один сдан,  - хотя бы один сдан, - хотя бы один сдан,  - ни одного не сдано.
в) Опыт –игра в шахматы.
События: - ни одного не сдано.
в) Опыт –игра в шахматы.
События: 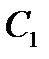 -выигрыш, -выигрыш,  - проигрыш. - проигрыш.
| ||||||||||||||||||||||||||||||||||||||||||
| 1.11. Записать полную группу событий в опыте. | ||||||||||||||||||||||||||||||||||||||||||
а) Опыт: Подбрасываются два игральных кубика.
Решение.
Полную группу событий образуют равновозможные элементарные исходы 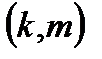  , представленные в таблице. Элементарный исход , представленные в таблице. Элементарный исход 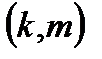 означает, что на первом кубике выпало означает, что на первом кубике выпало 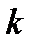 очков, а на втором очков, а на втором  очков. очков.
б) Опыт:сумма двух наудачу выбранных цифр равна 12. Дата добавления: 2015-08-10; просмотров: 88 | Нарушение авторских прав
|