| 3.1. Дописать формулировку теоремы и соответствующие формулы.
|
| Формула полной вероятности
|
Вероятность события  , которое может наступить лишь при появлении одного из несовместных событий (гипотез) , которое может наступить лишь при появлении одного из несовместных событий (гипотез)  образующих полную группу событий, равна … образующих полную группу событий, равна …
|
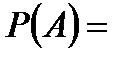 где
где  Здесь
Здесь  — вероятность — вероятность  - ой гипотезы, а - ой гипотезы, а  — условная вероятность события — условная вероятность события  при осуществлении данной гипотезы. при осуществлении данной гипотезы.
|
| Формула Байеса
|
Пусть событие  может наступить лишь при условии появления одного из несовместных событий (гипотез) может наступить лишь при условии появления одного из несовместных событий (гипотез)  образующих полную группу событий.
Если событие образующих полную группу событий.
Если событие  уже произошло, то вероятности гипотез могут быть переоценены по формулам Байеса: уже произошло, то вероятности гипотез могут быть переоценены по формулам Байеса:
|
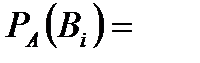
 где
где 
|
| | | |

 , которое может наступить лишь при появлении одного из несовместных событий (гипотез)
, которое может наступить лишь при появлении одного из несовместных событий (гипотез)  образующих полную группу событий, равна …
образующих полную группу событий, равна …
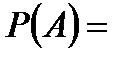 где
где  Здесь
Здесь  — вероятность
— вероятность  - ой гипотезы, а
- ой гипотезы, а  — условная вероятность события
— условная вероятность события  при осуществлении данной гипотезы.
при осуществлении данной гипотезы.
 может наступить лишь при условии появления одного из несовместных событий (гипотез)
может наступить лишь при условии появления одного из несовместных событий (гипотез)  образующих полную группу событий.
Если событие
образующих полную группу событий.
Если событие  уже произошло, то вероятности гипотез могут быть переоценены по формулам Байеса:
уже произошло, то вероятности гипотез могут быть переоценены по формулам Байеса:
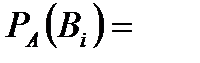
 где
где 