Решение задач на применение формулы полной вероятности и формулы Байеса

4.1. Разобрать решение, заполнив пропуски

Задача 1.Пешеход, идущий из некоторого пункта в пункт , стоит на разветвлении дорог и выбирает наугад один из возможных путей. Схема дорог изображена на рис. 11. Какова вероятность того, что пешеход попадет в пункт . Решение. Из схемы видно, что путь пешехода обязательно проходит через один из промежуточных пунктов 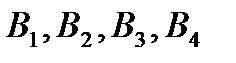. Обозначим через событие, состоящее в том, что при своем движении пешеход попадет в пункт . События образуют полную группу и очевидно, что они равновероятны (по условию один из путей выбирается произвольно). 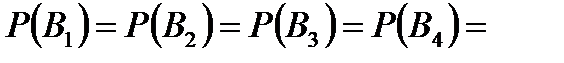Поэтому   Если пешеход попадет в пункт , то он сможет прийти в пункт , выбрав одно из трех равновозможных направлений движения.

Рис.11

Обозначим через событие, состоящее в том, что пешеход приходит в пункт . Тогда условная вероятность прийти в из пункта равна (по классическому определению вероятности).

Аналогично

По формуле полной вероятности

---

Дата добавления: 2015-08-10