| Понятие
| Определение
| Формула
|
Математическое
ожидание 
| Характеристика среднего значения случайной величины
| 
|
Дисперсия 
| Характеристика рассеяния возможных значений случайной величины вокруг математического ожидания
Математическое ожидание квадрата отклонения
|


|
Среднее квадратическое отклонение 
| Характеристика рассеяния возможных значений случайной величины вокруг математического ожидания
Квадратный корень из дисперсии
|

|
Свойства математического ожидания:
1.
 , ,  – const.
2. – const.
2.
 3.
3.  4.
4.

 независимые
5. независимые
5.

| Свойства дисперсии:
1.
 , ,  – const.
2. – const.
2.
 3.
3. 
 независимые
4. независимые
4.

 независимые независимые
|
| 2.1. Заполните пропуски в таблице:
|
| Закон распределения
| Формула
|
| Математическое
ожидание
| Дисперсия
| Среднее квадратическое отклонение
|
Равномерное распределение
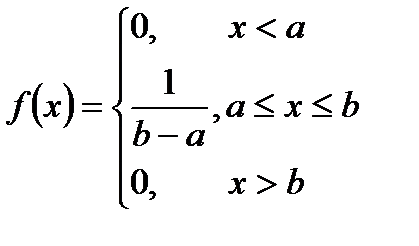
| 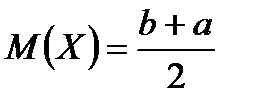
| 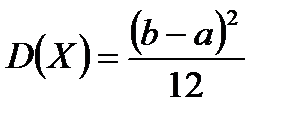
| 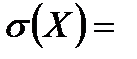
|
Показательное распределение

| 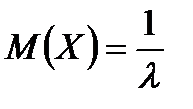
| 
| 
|
Нормальное распределение
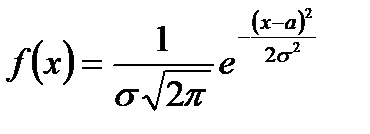
| 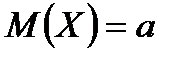
| 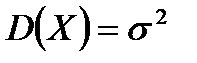
| 
|
| 2.2. Проанализируйте приведенное решение задачи и заполните пропуски
|
Задача13.
Решение.
Математическое ожидание: 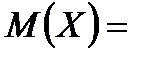 Дисперсию найдем по формуле
Дисперсию найдем по формуле  . .
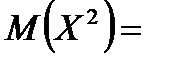
 Среднее квадратическое отклонение
Среднее квадратическое отклонение 
|
Задача14. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение для СВ в задаче 7 стр.8
Решение.
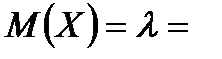
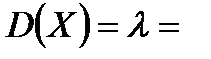

|
| | | | | | |








 ,
,  – const.
2.
– const.
2.
 3.
3.  4.
4.

 независимые
5.
независимые
5.

 ,
,  – const.
2.
– const.
2.
 3.
3. 
 независимые
4.
независимые
4.

 независимые
независимые
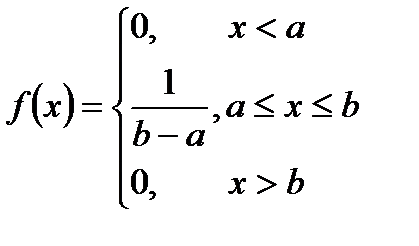
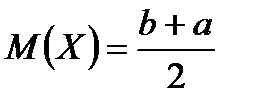
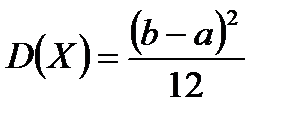
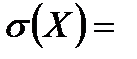

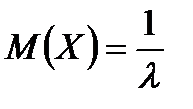


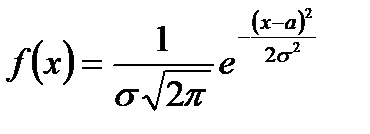
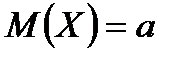
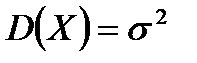

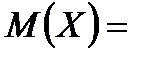 Дисперсию найдем по формуле
Дисперсию найдем по формуле  .
.
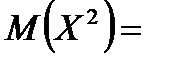
 Среднее квадратическое отклонение
Среднее квадратическое отклонение 
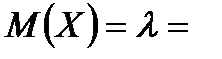
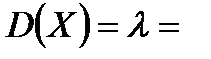

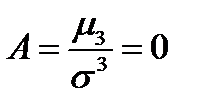 .
.
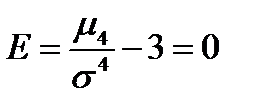 .
.