
|
Читайте также: |
Должно выполняется равенство  :
: 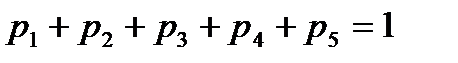 .
.
По условию 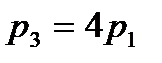 . Значит,
. Значит, 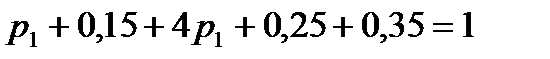 .
.
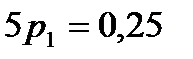 .
.
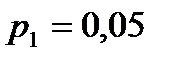 , следовательно
, следовательно 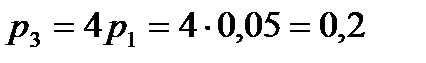 .
.
В прямоугольной системе координат строим точки 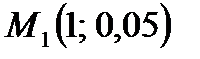 ,
, 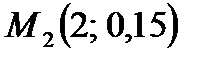 ,
, 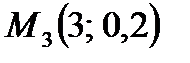 ,
, 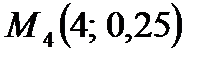 ,
, 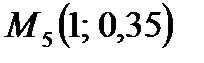 .
.
Ломанная 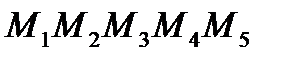 является многоугольником распределения данной СВ:
является многоугольником распределения данной СВ:
 .
.
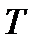 независимы и их вероятности соответственно равны 0,1; 0,2; 0,3. Найти закон распределения числа элементов, отказавших за время
независимы и их вероятности соответственно равны 0,1; 0,2; 0,3. Найти закон распределения числа элементов, отказавших за время 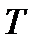 .
Решение.
СВ
.
Решение.
СВ 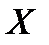 – число элементов, отказавших за время
– число элементов, отказавших за время 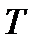 , значит
, значит 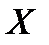 может принять значения:
может принять значения: 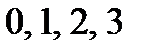 .
Найдем вероятности того, что отказавших элементов прибора за время
.
Найдем вероятности того, что отказавших элементов прибора за время 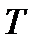 :
1) нет отказавших элементов, т.е. все элементы работают: и первый, и второй, и третий – событие
:
1) нет отказавших элементов, т.е. все элементы работают: и первый, и второй, и третий – событие 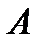 .
Пусть событие
.
Пусть событие 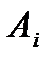 означает, что
означает, что 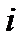 - ый элемент работает, а событие
- ый элемент работает, а событие 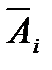 –
– 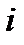 - ый элемент отказал.
Тогда, используя операции над событиями, получим
- ый элемент отказал.
Тогда, используя операции над событиями, получим 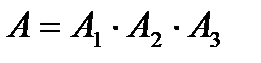 .
С учетом того, что отказы элементов независимы, имеем:
.
С учетом того, что отказы элементов независимы, имеем: 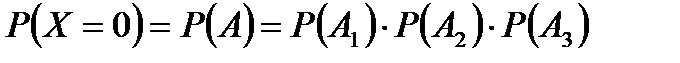 .
По условию задачи известно, что
.
По условию задачи известно, что 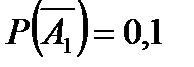 ;
; 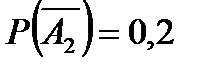 ;
; 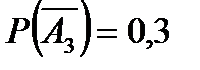 .
Тогда
.
Тогда
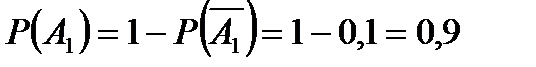 ;
; 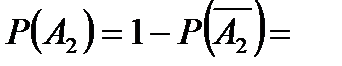
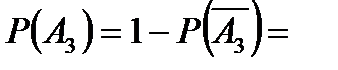 Таким образом,
Таким образом, 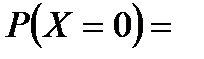 2) один элемент отказал, т.е. откажет первый элемент, а второй и третий работают или откажет второй элемент, а первый и третий работают, или откажет третий элемент, а первый и второй работают – событие
2) один элемент отказал, т.е. откажет первый элемент, а второй и третий работают или откажет второй элемент, а первый и третий работают, или откажет третий элемент, а первый и второй работают – событие 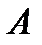 .
Пусть событие
.
Пусть событие 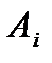 означает, что
означает, что 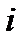 - ый элемент работает, а событие
- ый элемент работает, а событие 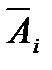 –
– 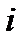 - ый элемент отказал.
Тогда используя операции над событиями, получим
- ый элемент отказал.
Тогда используя операции над событиями, получим 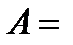 Итак, с учетом того, что отказы элементов независимы, а предложенные варианты отказа одного элемента не могут произойти одновременно, то имеем:
Итак, с учетом того, что отказы элементов независимы, а предложенные варианты отказа одного элемента не могут произойти одновременно, то имеем:
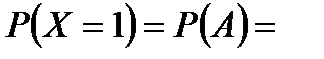 3) два элемента, т.е. первый элемент работает, а второй и третий отказали или второй элемент работает, а первый и третий отказали, или работает третий элемент, а первый и второй отказали – событие
3) два элемента, т.е. первый элемент работает, а второй и третий отказали или второй элемент работает, а первый и третий отказали, или работает третий элемент, а первый и второй отказали – событие 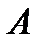 .
Пусть событие
.
Пусть событие 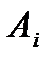 означает, что
означает, что 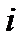 - ый элемент работает, а событие
- ый элемент работает, а событие 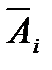 –
– 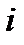 - ый элемент отказал.
Тогда используя операции над событиями, получим
- ый элемент отказал.
Тогда используя операции над событиями, получим 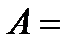 Итак, с учетом того, что отказы элементов независимы, а предложенные варианты отказа двух элементов не могут произойти одновременно, то имеем:
Итак, с учетом того, что отказы элементов независимы, а предложенные варианты отказа двух элементов не могут произойти одновременно, то имеем:
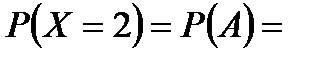 4) все три элемента, т.е. все элементы отказали: и первый, и второй, и третий – событие
4) все три элемента, т.е. все элементы отказали: и первый, и второй, и третий – событие 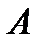 .
Пусть событие
.
Пусть событие 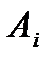 означает, что
означает, что 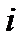 - ый элемент работает, а событие
- ый элемент работает, а событие 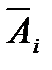 –
– 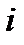 - ый элемент отказал.
Тогда используя операции над событиями, получим
- ый элемент отказал.
Тогда используя операции над событиями, получим 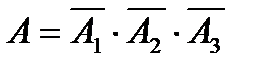 .
Итак,
.
Итак, 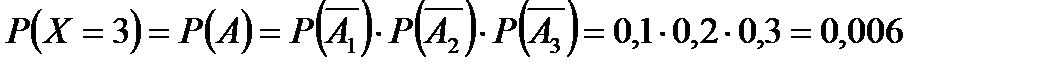 .
Напишем искомый закон распределения:
.
Напишем искомый закон распределения:
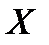
| ||||
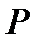
| 0,006 |
Контроль 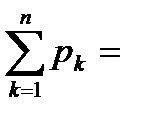
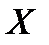 – числа нестандартных деталей среди четырех отобранных.
2. Построить многоугольник полученного распределения.
Решение.
СВ
– числа нестандартных деталей среди четырех отобранных.
2. Построить многоугольник полученного распределения.
Решение.
СВ 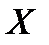 – число нестандартных деталей среди четырех отобранных, значит множество возможных значений
– число нестандартных деталей среди четырех отобранных, значит множество возможных значений 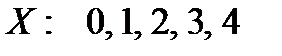 .
Найдем вероятности возможных значений
.
Найдем вероятности возможных значений 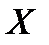 , пользуясь формулой Бернулли
, пользуясь формулой Бернулли  .
Вероятность появления нестандартной детали в каждом случае равна 0,1.
Найдем вероятности того, что среди отобранных деталей:
1) нет нестандартных.
.
Вероятность появления нестандартной детали в каждом случае равна 0,1.
Найдем вероятности того, что среди отобранных деталей:
1) нет нестандартных.
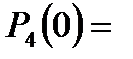 2) одна нестандартная.
2) одна нестандартная.
 3) две нестандартные детали.
3) две нестандартные детали.
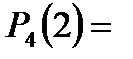 4) три нестандартные детали.
4) три нестандартные детали.
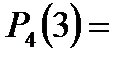
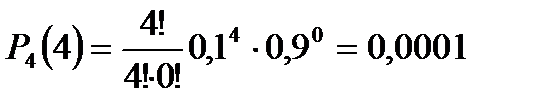 .
Напишем искомый биномиальный закон распределения:
.
Напишем искомый биномиальный закон распределения:
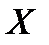
| |||||
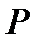
| 0,0001 |
Контроль 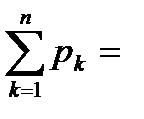
Построим многоугольник распределения.

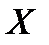 – число извлеченных белых шаров. Найти закон распределения дискретной СВ
– число извлеченных белых шаров. Найти закон распределения дискретной СВ 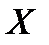 .
Решение.
СВ
.
Решение.
СВ 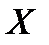 – число извлеченных белых шаров среди двух отобранных, значит
– число извлеченных белых шаров среди двух отобранных, значит 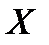 имеет следующие возможные значения:
Найдем вероятности возможных значений
имеет следующие возможные значения:
Найдем вероятности возможных значений 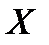 , пользуясь формулой
, пользуясь формулой  ,
где
,
где  — число всех шаров, из которых
— число всех шаров, из которых  — белые шары;
— белые шары;  — число отобранных шаров, a
— число отобранных шаров, a  — число белых шаров, оказавшихся в выборке.
— число белых шаров, оказавшихся в выборке.
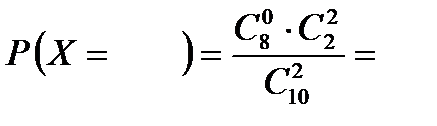
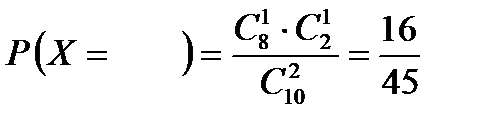 .
.
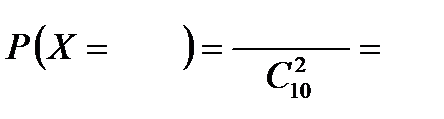 Получили гипергеометрическое распределение:
Получили гипергеометрическое распределение:
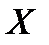
| |||
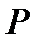
|
Контроль 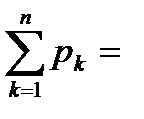
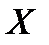 – число очков, выпавших при одном подбрасывании кубика, значит
– число очков, выпавших при одном подбрасывании кубика, значит 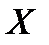 имеет следующие возможные значения:
Найдем вероятности возможных значений
имеет следующие возможные значения:
Найдем вероятности возможных значений 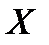 , пользуясь формулой
, пользуясь формулой  ,
где
,
где  — все возможные значения СВ,
— все возможные значения СВ,  — количество возможных значений СВ.
Запишем искомое равномерное распределение:
— количество возможных значений СВ.
Запишем искомое равномерное распределение:
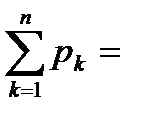 Построим многоугольник распределения:
Построим многоугольник распределения:
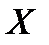 – число страниц с опечатками, т.е.
– число страниц с опечатками, т.е. 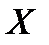 имеет следующие возможные значения:
имеет следующие возможные значения: 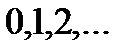 .
Событие
.
Событие  - появление страницы с опечатками. Получается, что производится большое количество повторных независимых испытаний -
- появление страницы с опечатками. Получается, что производится большое количество повторных независимых испытаний - 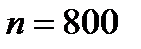 , в каждом из которых событие
, в каждом из которых событие  имеет очень малую вероятность
имеет очень малую вероятность 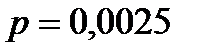 .
Тогда для вычисления вероятности, что событие появится ровно
.
Тогда для вычисления вероятности, что событие появится ровно 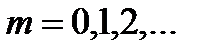 раз, можно воспользоваться формулой
раз, можно воспользоваться формулой  ,
,
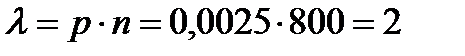 - параметр распределения Пуассона, которым приближенно заменяется биномиальное распределение.
- параметр распределения Пуассона, которым приближенно заменяется биномиальное распределение.
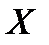
| … | 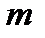
| … | ||||
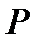
| 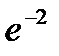
| 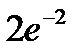
| 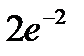
| 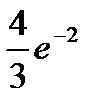
| … | 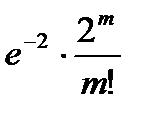
| … |
Контроль 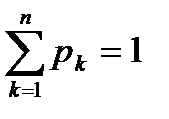 : принимая во внимание разложение функции
: принимая во внимание разложение функции 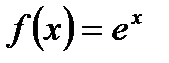 в степенной ряд
в степенной ряд 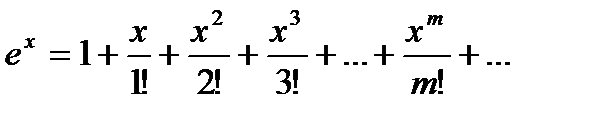 и вытекающего отсюда равенства
и вытекающего отсюда равенства 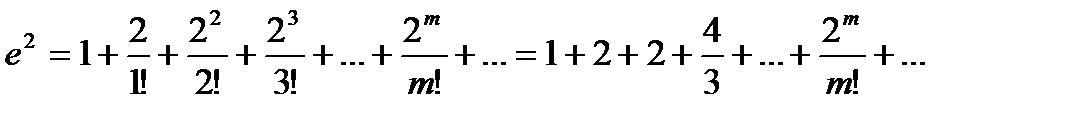 , получаем
, получаем 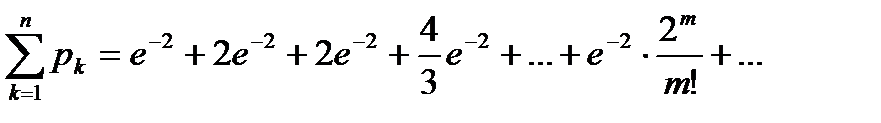
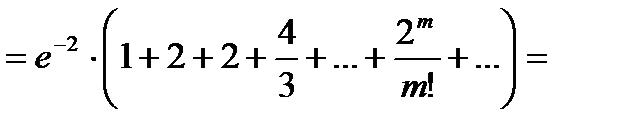
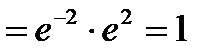 .
.
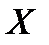
| ||||
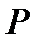
| 0,2 | 0,4 | 0,3 | 
|
Найти функцию распределения СВ и построить ее график.
Дата добавления: 2015-08-10; просмотров: 1255 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Решение. | | | Решение. |