Способы задания непрерывной СВ

Функция распределения вероятностей (интегральная функция).
Плотность распределения вероятностей (дифференциальная функция)
1.1. Заполните пропуски
Свойства функции распределения :	Свойства плотности распределения :
1. 2. Функция распределения является неубывающая, т.е. если , то выполняется неравенство 3. Функция распределения в точке непрерывна слева, т.е. 4. и   5. 6.	1.   2.   3. 4. .
1.2. Заполните таблицу соответствия, закон распределения выберите из списка: а) нормальное распределение; б) равномерное распределение; в) показательное распределение.
Закон распределения	Плотность распределения вероятности	Функция распределения	Вероятность попадания СВ в интервал
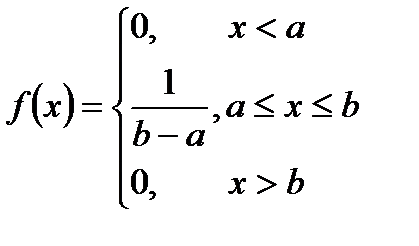
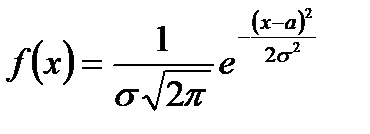
1.3. Проанализируйте приведенное решение задачи и заполните пропуски
Задача1.Является ли функцией распределения некоторой случайной величины функция ?   Решение. Проверим выполнение свойств функции распределения. Все значения этой функции принадлежат отрезку , т. е. Функция является …: в промежутке она постоянна, а именно равна нулю, (см. рис.) в промежутке … в промежутке … Функция непрерывна в каждой точке области ее определения, т.е. непрерывна на промежутке … поэтому непрерывна и слева, т. е. выполняется равенство Выполняются и равенства: и Следовательно, функция удовлетворяет всем свойствам, характерным для функции распределения. Значит, данная функция является функцией распределения некоторой случайной величины .
Задача2.Функция распределения случайной величины задана выражением: Написать выражение для плотности распределения. Решение. . при , тогда . при , тогда при , тогда Таким образом,
Задача3. Плотность распределения случайной величины задана выражением: . Найти значение . Решение. Найдем из основного свойства функции : . . , . . Вычислим интеграл   Подставим значение в : .
Задача 4. Задана плотность непрерывной случайной величины : Найти функцию распределения . Решение. Используем формулу . Если , то . Если , то     Если , то     Итак, искомая функция распределения
Задача5. Плотность распределения случайной величины задана выражением: . Найти значение . Определить функцию распределения. Найти вероятность . Решение. Найдем из основного свойства функции : . . . . . Вычислим несобственный интеграл   . Найдем функцию распределения , используя формулу . Если , то . Если , то     Итак, искомая функция распределения   Найдем вероятность .

Задача 6. Автобусы идут строго по расписанию. Интервал движения 7 мин. Найти: а) вероятность того, что пассажир, подошедший к остановке, будет ожидать очередной автобус менее двух минут; б) вероятность того, что пассажир, подошедший к остановке, будет ожидать очередной автобус не менее трех минут.   Решение. По условию задачи непрерывная случайная величина время ожидания пассажира равномерно распределена между приходами двух автобусов. Дифференциальная функция равномерного распределения 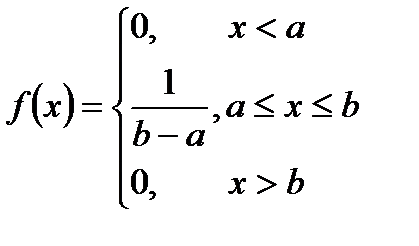.Длина интервала распределения случайной величины равна . Получаем, что     а) время ожидания будет менее двух минут, если случайная величина попадает в интервал . Вероятность попадания в заданный интервал найдем по формуле: . б) время ожидания будет не менее трех минут (т.е. от трех до семи мин.), если случайная величина попадает в интервал . Вероятность попадания в заданный интервал  

Задача7. Время в годах безотказной работы прибора подчинено показательному закону, т.е. плотность распределения этой случайной величины такова: . Определить: а) вероятность того, что прибор проработает не более года; б) вероятность того, что прибор безотказно проработает 3 года. Решение. а) определим вероятность того, что прибор проработает не более года, то есть безотказная работа от 0 до 1 года. Используем известную формулу для показательного распределения: .   б) определим вероятность того, что прибор безотказно проработает 3 года, то есть 3 или более лет (как минимум 3 года).    

Задача8. По данным страховых агентств некоторой страны вероятность того, что человек доживёт до 70 лет, равна 0,32. Какова вероятность того, что случайный новорожденный доживёт до 22 лет? Решение. Продолжительность жизни человека подобна длительности работы механизма - до первого отказа. Поэтому используем показательное распределение. Плотность вероятности при показательном распределении: . Найдем параметр . По условию . Тогда   Ответ:0,7

Задача9. Текущая цена акции может быть смоделирована с помощью нормального закона распределения с математическим ожиданием 15 ден. ед. и средним квадратическим отклонением 0,2 ден. ед. Найти вероятность того, что цена акции: а) не выше 15,3 ден. ед.; ) не ниже 15,4 ден. ед.; в) от 14,9 до 15,3 ден. ед. С помощью «правила трех сигм» найти границы, в которых будет находиться текущая цена акции.   Решение. Так как и , то .       По «правилу трех сигм» , . Решим неравенство .   Окончательно   Ответ: , ,

Задача10. Автомат изготавливает детали, которые считаются годными, если отклонение от контрольного размера по модулю не превышает 0,8 мм. Каково наиболее вероятное число годных деталей из 150, если случайная величина распределена нормально с мм? Решение. Каково наиболее вероятное число годных деталей найдем из неравенства: . , вероятность отклонения от контрольного размера. Найдем вероятность отклонения при и .     Откуда .

Задача11. Рост взрослых мужчин является случайной величиной, распределенной по нормальному закону. Пусть математическое ожидание ее равно 175 см, а среднее квадратическое отклонение - 6 см. Определить вероятность того, что хотя бы один из наудачу выбранных пяти мужчин будет иметь рост от 170 до 180 см.   Решение. Событие хотя бы один из наудачу выбранных пяти мужчин будет иметь рост от 170 до 180 см. . Найдем вероятность того, что рост мужчины будет принадлежать интервалу по формуле .     Ответ: 0,9898

Задача12. Длина X некоторой детали представляет собой случайную величину, распределенную по нормальному закону распределения, и имеет среднее значение 20 мм и среднее квадратическое отклонение – 0,2 мм. Необходимо: найти вероятность того, что величина отклонения не превышает 0,1 мм; определить, какой процент составляют детали, отклонение которых от среднего значения не превышает 0,1 мм; найти, каким должно быть задано отклонение, чтобы процент деталей, отклонение которых от среднего не превышает заданного, повысился до 54%; найти интервал, симметричный относительно среднего значения, в котором будет находиться с вероятностью 0,95. записать выражение плотности распределения, построить график; Решение. Вероятность того, что абсолютная величина отклонения меньше положительного числа 0,1 найдем по формуле .   Поскольку вероятность отклонения, меньшего 0,1 мм, равна 0,383, то отсюда следует, что в среднем 38,3 детали из 100 окажутся с таким отклонением, т.е. 38,3%.

Поскольку процент деталей, отклонение которых от среднего не превышает заданного, повысился до 54%, то . или По таблице значений функции Лапласа находим   Так как искомый интервал симметричен относительно среднего значения , то его можно определить как множество значений , удовлетворяющих неравенству или .   По условию вероятность нахождения в искомом интервале равна 0,95, значит . С другой стороны или По таблице значений функции Лапласа находим   Искомый интервал: (19,608; 20,392).   Плотность вероятности случайной величины X, распределенной по нормальному закону находим по формуле:   Для построения графика функции найдем: 1) наибольшее значение функции: 2) точки перегиба горизонтальная асимптота

---

Дата добавления: 2015-08-10