Средние величины

Средней величиной в статистике называется обобщающий показатель, характеризующий типичный уровень явления в конкретных условиях места и времени, отражающий величину выросшего признака в расчете на единицу качественно однородной совокупности.

Средний показатель отражает то общее, что характерно (типично) для всех единиц изучаемой совокупности, в то же время он игнорирует различия отдельных единиц.

Выбор вида средней определяется экономическим содержанием определенного показателя и исходных данных. В каждом конкретном случае применяется одна из средних величин: арифметическая, гармоническая, геометрическая и т.д.

Наиболее распространенным видом средних величин является средняя арифметическая.Она применяется в тех случаях, когда объем варьирующего признака для всей совокупности является суммой значений признаков отдельных ее единиц.

Чтобы рассчитать среднюю арифметическую, нужно сумму всех значений признаков разделить на их число.

Средняя арифметическая величина применяется в форме простой средней и взвешенной средней.

Средняя арифметическая простая равна простой сумме отдельных значений осредняемого признака, делимой на общее число этих значений (она применяетсяв тех случаях, когда имеются не сгруппированные индивидуальные значения признака).

, (1.4)

где Х₁,X₂,Х_n – индивидуальные значения варьирующего признака (варианты);

n - число единиц совокупности.

Для расчета средних сгруппированных индивидуальных значений признака совокупности применяется расчет средней арифметической взвешенной.

Средняя величина из вариантов, которые повторяют различное число раз, или, имеют различный вес, называются взвешенной. В качестве весов выступают численности единиц в разных группах совокупности.

Средняя арифметическая взвешенная – средняя сгруппированных величин выполняется по формуле

, (1.5)

где X1,X2, X п- отдельные значение признака;

f₁ f₂ f₃ - веса/частоты повторения одинаковых признаков,

Σ xf - сумма произведений величин признаков на их частоты;

Σf - общая численность единиц совокупности.

Вычисление средней арифметической взвешенной из групповых средних Хгр осуществляется по формуле

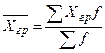, (1.6)

где f- число единиц каждой группе.

Если значения определяемого признака заданы в виде интервалов («от – до»), т.е. интервальных видов распределения, то при росте средней арифметической величины в качестве значений признаков в группах принимают середины этих интервалов. После того как найдены середины интервалов, вычисления делают так же при расчете средней взвешенной.

Дата добавления: 2015-08-02