Индексы

Под индексом понимают относительный показатель, характеризующий изменение величины к.л. явления во времени, пространстве или по сравнению с любым эталоном (нормативом, планом и т.д.).

В теории индексного метода применяют следующие обозначения:

1 – подстрочный символ показателя текущего (отчетного) периода;

0 – подстрочный символ предшествующего (базисного) периода;

i - индивидуальный индекс;

I – сводный (агрегатный) индекс

Р – цена (розничная или оптовая);

q –количество (товара или выпущенной продукции);

z – себестоимость продукции;

t – трудоемкость единицы продукции;

pq –товарооборот;

zq – издержки производства;

По степени охвата единиц совокупности индексы делятся на 2 класса: индивидуальные и общие.

Индивидуальные индексы служат для характеристики изменения отдельных элементов сложного явления.

Общий индексотражает изменение всех элементов сложного явления. Под сложным явлением понимают такую статистическую совокупность, отдельные элементы которой непосредственно не подлежат суммированию (цепи на разные группы продуктов и т.д.).

Общие индексы м.б. построены двумя способами: как средние из индивидуальных и как агрегатные.

Агрегатный индекс является основной формой индекса. Агрегатным он называется потому, что его числитель и знаменатель представляют набор непосредственно несоизмеримых и не поддерживающихся суммированию элементов – сумму произведений двух величин, одна из которых меняется, а другая остается неизменной в числителе и в знаменателе (вес индекса).

Индивидуальные индексы определяют вычислением отношения двух индексированных величин.

Так индивидуальный индекс цены рассчитывается по формуле

, (5.1)

где P₁ – объем продукции в текущем периоде, т. руб.;

P₀ – объем продукции в базисном периоде, т. руб.

Индивидуальный индекс физического объема:

, (5.2)

где q₁ – объем продукции в натуральном выражении текущего года;

q₀ - объем продукции в натуральном выражении базисного периода.

Определение стоимости продукции базисного периода 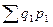к стоимости продукции текущего периода представляет собой агрегатный индекс стоимости

(5.3)

Этот индекс показывает, во сколько раз возросла (уменьшилась) стоимость продукции отчетного периода по сравнению с базисным.

Если продукцию (товары) сравниваемых периодов оценивать одним и тем же базисным ценам p₀, то такой индекс отразит изменения только одного фактора – индексируемого показателя q₀ и будет представлять собой агрегатный индекс физического объема продукции

. (5.4)

Индекс физического объема продукции показывает, во сколько раз объем продукции изменился в отчетном периоде по сравнению с базисным периодом.

Агрегатный индекс цен исчисляют по формуле:

. (5.5)

Индекс цен показывает, во сколько раз возрос (уменьшился) в среднем уровень цен отчетного периода по сравнению с базисным.

Разность числителя и знаменателя каждого индекса в правой части выражает изменение общей абсолютной величины под влиянием изменения одного фактора.

Общее изменение

.

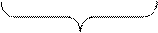
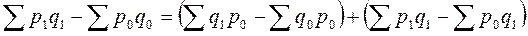D_qp

а) изменение товарооборота за счет цен: D_р = åp₁^. q₁ - å p₀ ^. q₁;

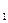
б) изменение товарооборота за счет объема: D_q = åp ^. q - å p₀ ^. q₀.

Дата добавления: 2015-08-02