Читайте также:
|
Вариация - это различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени.
Средняя величина дает обобщающую характеристику признака изучаемой совокупности, но она не раскрывает строения совокупности. Средняя не показывает, как располагаются около нее варианты осредняемого признака, сосредоточены ли они вблизи средней величины или значительно отклоняются от нее.
Потому возникает необходимость измерять вариацию признака в совокупностях. Для этой цели в статистике применяют ряд обобщающих показателей.
К показателям вариации относятся: размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение, коэффициент вариации.
Размах вариации (R) - разность между максимальным и минимальным значением признака в совокупности (см. формулу 1.3).
Среднее линейное отклонение (
) представляет собой среднюю арифметическую абсолютных значений отклонений отдельных вариантов от их средней арифметической (при этом виде предполагают, что среднюю вычисляют из варианта.
Среднее линейное отклонение рассчитывают по формуле:
а) для несгруппированных данных
, (2.1)
где х– отдельные значения признака (вариант);
- средняя величина по совокупности;
n – число членов ряда.
б) для сгруппированных данных
, (2.2)
где 
- сумма частот вариационного ряда.
Дисперсия (
) – это средний квадрат отклонений вариантов от их средней величины.
а) Простая дисперсия для несгруппированных данных
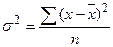, (2.3)
б) взвешенная дисперсия для вариационного ряда
. (2.4)
Среднее квадратическое отклонение (
) равно корню квадратному из дисперсии
а) для негруппированных данных
, (2.5)
б) для вариационного ряда
. (2.6)
Среднее квадратическое отклонение показывает, на сколько в среднем откланяются конкретные варианты от их среднего значения.
Коэффициент вариации (γ) – выражен в % отношении среднего квадратического отклонения к средней арифметической
. (2.7)
Совокупность считается количественно однородной, если коэффициент вариации не превышает 33 %.
Дата добавления: 2015-08-02; просмотров: 49 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Пример 2 | | | Правило сложения дисперсий |