Правило сложения дисперсий

Общая дисперсия () измеряет вариацию признака по всей совокупности под влиянием факторов, обусловивших эту вариацию.

Она равна среднему квадрату отклонений отдельных значений признака х от общей средней и может быть вычислена как простая по (формуле 2.3) или взвешенная дисперсия (по формуле 2.4).

Межгрупповая дисперсия (δ2) характеризует систематическую вариацию результативного порядка, обусловленную влиянием факторного признака, положенного в основание группировки.

Определение по формуле

δ2 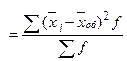, (2.8)

где xi – средняя по каждой группе;

xоб– средняя по совокупности

Внутригрупповая дисперсия () отражает случайную вариацию, т.е. часть вариации, обусловленную влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки

а) внутригрупповая дисперсия для негруппированных данных может быть исчислена по формуле

, (2.9)

б) для сгруппированных данных

. (2.10)

На основании внутригрупповой дисперсии можно определить общую среднюю из внутригрупповых дисперсий

.

Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповых дисперсий

.

Дата добавления: 2015-08-02