
Читайте также:
|
Круглая тонкая пластинка радиуса  однородно заряжена с поверхностной плотностью
однородно заряжена с поверхностной плотностью  .
.
Найдите модуль напряженности электрического поля на оси пластинки, как функцию расстояния  от ее центра. Рассмотрите предельные случаи
от ее центра. Рассмотрите предельные случаи  и
и  .
.
Решение.
Представим круглую пластинку в виде набора узких концентрических колец радиуса  и ширины
и ширины  (см. рис.).
(см. рис.).

|
Заряд одного такого элементарного кольца  равен:
равен:
 ,
,
где 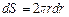 площадь этого кольца.
площадь этого кольца.
Используя формулу для напряженности поля на оси кольца из примера 1.7., запишем напряженность поля в произвольной точке  с координатой
с координатой  :
:
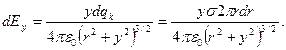
Векторы  направлены одинаково для всех колец пластинки (по оси
направлены одинаково для всех колец пластинки (по оси  , так как заряд пластинки положительный). Применив принцип суперпозиции для напряженности, найдем
, так как заряд пластинки положительный). Применив принцип суперпозиции для напряженности, найдем  :
:


Построим график зависимости  :
:

Рассмотрим предельные случаи:
1) при 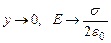 - что соответствует полю бесконечной равномерно заряженной плоскости;
- что соответствует полю бесконечной равномерно заряженной плоскости;
2) при  , учитывая что
, учитывая что 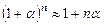 , поле пластинки можно привести к виду:
, поле пластинки можно привести к виду:

то есть на больших расстояниях поле круглой пластинки соответствует полю точечного заряда, помещенного в ее центр.
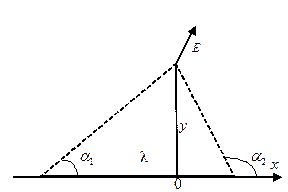 Пример 1.14
Пример 1.14
Найти напряженность 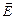 электрического поля, созданного отрезком тонкой, однородно заряженной с линейной плотностью
электрического поля, созданного отрезком тонкой, однородно заряженной с линейной плотностью  нити в точке наблюдения c координатами
нити в точке наблюдения c координатами  ,
,  (см. рис.). Углы с осью x, под которыми видна точка наблюдения из концов отрезка
(см. рис.). Углы с осью x, под которыми видна точка наблюдения из концов отрезка  ,
,  и расстояние y - известны.
и расстояние y - известны.
Решение.
Вклад в напряженность поля от элемента отрезка dx равен  . Поля от разных элементов отрезка
. Поля от разных элементов отрезка  отличаются как величиной, так и направлением. Поэтому для нахождения результирующего поля проинтегрируем проекции элементарных полей
отличаются как величиной, так и направлением. Поэтому для нахождения результирующего поля проинтегрируем проекции элементарных полей  и
и  . Для удобства интегрирования выразим переменные величины r и x через угол
. Для удобства интегрирования выразим переменные величины r и x через угол  по соотношениям (см.рис.)
по соотношениям (см.рис.) 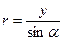 и
и  ,
,  . При этом
. При этом 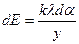 и для проекций Ex и Ey получим:
и для проекций Ex и Ey получим:
 ,
, 

Полученные формулы включают в себя все результаты расчета полей однородно заряженных отрезков. Приведем наиболее часто используемые:
Поле на перпендикуляре, проведенном из середины отрезка:
 ,
, 

|
Поле бесконечного отрезка:
 ,
, 
 ,
, 
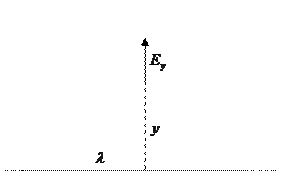
|
Поле полубесконечного отрезка в точках плоскости перпендикулярной отрезку и проходящей через его торец:
 ,
, 




Дата добавления: 2015-08-10; просмотров: 62 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Пример 1.12 | | | Пример 1.15 |