Пример 1.5

На единицу длины тонкого однородно заряженного стержня АВ, имеющего форму дуги окружности радиуса R с центром в точке О, приходится заряд 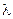. Найдите модуль напряженности электрического поля в точке О, если угол АОВ равен .

Решение.

Выберем оси координат так, чтобы начало координат совпадало с точкой О, а ось у была симметрично расположена относительно концов дуги АВ (рис.).

Разобьем стержень на элементарные участки длины dl с зарядом , который можно рассматривать как точечный.

Найдем напряженность поля, создаваемого зарядом этого элементарного участка стержня в точке 0:

,

где - радиус вектор, направленный от элемента dl к точке, напряженность которой вычисляется. Напряженность результирующего поля найдем, воспользовавшись принципом суперпозиции. В силу симметрии результирующее поле будет направлено вдоль оси у (рис.). Запишем выражение для проекции :

.

Приведем правую часть последнего уравнения к одной переменной интегрирования – углу (учитывая, что )

.

Проинтегрировав левую часть полученного уравнения от до E, а правую от до , найдем модуль напряженности электрического поля, создаваемого в точке О дугой АВ:

.

Рассмотрим специальные случаи использования формулы для расчета поля, создаваемого частью дуги окружности в ее центре :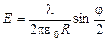

а) Модуль напряженности электрического поля, создаваемого 1/4 части дуги окружности радиуса R в ее центре:

.

б) Модуль напряженности электрического поля, создаваемого тонким полукольцом радиуса R в его центре:

.

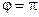
в) Модуль напряженности электрического поля, создаваемого тонким кольцом радиуса R в его центре:

.

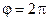
г) Модуль напряженности электрического поля в центре тонкого кольца радиуса R, если половины этого кольца заряжены разноименными зарядами с линейными плотностями заряда 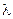и .

Напряженность электрического поля, создаваемого каждой из половинок равна:

,

.

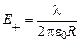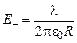Согласно принципу суперпозиции найдем результирующее поле в центре

.

Из рисунка видно, что направления векторов и совпадают, поэтому результирующее поле в центре такого кольца равно

.

Дата добавления: 2015-08-10