Принцип суперпозиции

Закон Кулона. Напряженность электрического поля.

Принцип суперпозиции

(теория, вопросы, упражнения)

1. Согласно современным представлениям, электрическое взаимодействие между телами осуществляется посредством электромагнитных полей. Свойство тела создавать в окружающем пространстве электромагнитное поле количественно характеризуется скалярной физической величиной называемой электрический заряд. Свойство силового поля одного заряженного тела действовать на другие заряженные тела характеризуется векторной физической величиной называемой напряженность электрического поля. Основными законами, позволяющими описать электрическое взаимодействие неподвижных заряженных тел, являются закон Кулона и принцип суперпозиции. Для описания действия электрических сил вводят понятия точечного и пробного зарядов.

Точечными зарядами называются заряженные тела, размеры которых малы по сравнению с расстояниями между телами (т.е. в области пространства,занимаемого такими заряженными телами электрическое поле однородно).

Пробными зарядами называются заряженные тела, внесение которых в электрические поля других тел не приводит к их искажению (т.е. величина заряда настолько мала, что не приводит к смещению зарядов на окружающих телах).

2. Закон Кулона определяет силы взаимодействия двух неподвижных точечных зарядов и , расположенных на расстоянии r₁₂ друг от друга

.

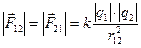Здесь - сила, действующая на первый заряд со стороны второго, - сила, действующая на второй заряд со стороны первого (эти силы удовлетворяют третьему закону Ньютона, т.е. являются силами действия и противодействия). Величины сил пропорциональны величинам зарядов и и обратно пропорциональны - квадрату расстояния между ними. Силы всегда направлены вдоль прямой, соединяющей эти заряды. Они являются силами притяжения, если знаки зарядов противоположны и силами отталкивания, если знаки зарядов одинаковы (см. рис.1). Свойства сил взаимодействия точечных зарядов отражает векторная форма закона Кулона:

 

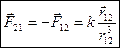
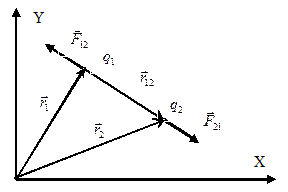
Рис.1

В системе СИ коэффициент к в законе Кулона с учетом единицы заряда принято представлять в виде:

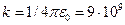Нм²/Кл²

где 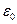-электрическая постоянная.

Упражнение 1.

Покажите, как можно количественно сравнить электрические заряды двух тел.

Решение:

Пусть q₁ и q₂ величины зарядов электрических тел, которые необходимо сравнить. Возьмем третье заряженное тело, заряд которого обозначим Q. И в точке на расстоянии r от него, которое велико по сравнению с размерами всех трех тел, поместим последовательно тела, заряды которых мы сравниваем. Измеряя силы и , с которыми сравниваемые заряды будут взаимодействовать последовательно с зарядом Q, на основании закона Кулона утверждаем, что и будут иметь либо одинаковые, либо противоположные направления, а отношение их величин 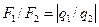не зависит ни от расположения заряда Q ни от его величины. Поэтому отношение F₁/F₂ служит мерой самих пробных зарядов, причем, если направления сил и совпадают, алгебраические знаки зарядов совпадают.

3. Исследования взаимодействия заряженных тел выявили следующие фундаментальные свойства зарядов:

- Электрический заряд существует в двух формах - он может быть положительным или отрицательным.

- Электрический заряд подчиняется закону сохранения: полный электрический заряд системы тел остается неизменным, если заряженные тела не пересекают поверхность, ограничивающую эту систему. При этом неизменным остается только полный заряд, а не положительный и отрицательный в отдельности. Например, при рождении пары электрон – позитрон в системе возникают заряды, но полный заряд сохраняется.

- Электрический заряд – величина релятивистки инвариантная: величина заряда любого тела не зависит от того, как это тело движется.

- В природе существует минимальный по величине заряд. Его называют элементарным и обозначают e. Любой электрический заряд кратен элементарному заряду

()

То, что является естественной единицей измерения заряда, по историческим причинам не было использовано, и в системе СИ за единицу заряда была выбрана величина, равная 6,2418 и получившая название кулон. Поэтому для величины элементарного заряда получим:

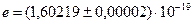Кл

Упражнение 2.

Найдите силу, с которой точечный заряд Q будет действовать на точечный заряд , если на точечный заряд , помещенный в ту же точку пространства он действует с силой .

Решение:

Построив вектор из точки нахождения заряда в точку помещения заряда q₂, запишем выражение для силы на основе закона Кулона 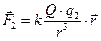. Аналогично для заряда , помещенного в ту же самую точку, и, сравнивая выражения для этих сил, получим .

4. Векторная физическая величина, модуль которой численно равен силе, действующей на единичный положительный неподвижный пробный заряд, помещенный в некоторой точке наблюдения, а направление совпадает с направлением этой силы, называется напряженностью электрического поля в рассматриваемой точке и обозначается вектором ,

Силу, действующую на любой точечный заряд q, покоящийся в поле , представим в векторном виде:

Упражнение 3:

Найдите напряженность электрического поля точечного заряда Q.

Решение:

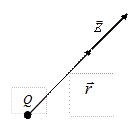
Поместим вблизи заряда Q точечный заряд q, в положение, задаваемое вектором относительно заряда Q, как показано на рис.2. Силу, действующую на заряд q, запишем в векторной форме как: .

Рис.2

Напряженность электрического поля точечного заряда в рассматриваемой точке равна 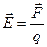, откуда:

5. Сила, действующая на заряд q со стороны нескольких зарядов равна векторной сумме сил:

или на языке напряженностей: ,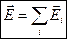

где -поле i -го заряда в точке нахождения заряда q. Этот закон, называемый принципом суперпозиции, фактически утверждает, что сила взаимодействия двух точечных зарядов не зависит от наличия в их окрестности других заряженных тел.

6. Часто распределение зарядов на телах описывается непрерывным распределением электричества. Распределение электричества по объему пространства задается пространственной плотностью заряда , по поверхности - поверхностной плотностью заряда , вдоль линии – линейной плотностью заряда :

dq = ρ dV, dq = σ dS, dq = λ dl.

7. Для графического изображения векторных полей используют силовые линии (линии напряженности) поля, которые проводятся по следующим правилам: касательная к силовой линии направлена вдоль вектора в каждой точке; густота силовых линий пропорциональна напряженности в данной области пространства. Силовые линии начинаются и заканчиваются на зарядах, а в пустом пространстве непрерывны. Число линий начинающихся и заканчивающихся на зарядах пропорционально их абсолютной величине.

Вопросы

1.1 Три заряда расположены в вершинах равнобедренного прямоугольного треугольника. В вершинах острых углов находятся заряды + q, , а в вершине прямого угла заряд +2q (см. рис.3). Определить какой из представленных на рисунке векторов совпадает с направлением напряженности поля в середине гипотенузы.

 

Рис.3

Ответ:

Напряженности полей, создаваемые зарядами q, равны по величине и направлены в сторону отрицательного заряда. Если обозначить длину гипотенузы 2a, то каждая из этих напряженностей равна 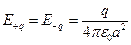и их сумма составляет 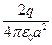. Это же значение имеет и поле заряда + 2q, направленное вдоль луча проведенного из прямого угла в середину гипотенузы. Напряженность результирующего поля направлена параллельно катету в направлении 3.

1.2 Дана система N точечных зарядов. Какой физический смысл имеют выражения:

а)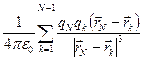

б)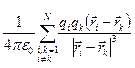

Ответ:

а) Вынесем q_N из под знака суммирования 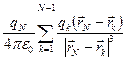, тогда каждое слагаемое под знаком суммы представляет вектор напряженности k -го заряда в точке нахождения N -го. А вся сумма – результирующее поле (N-1) зарядов в этой точке _{N-1}. Выражение а) представится как q_{N { N-1}}, т.е.равно силе, действующей на заряд q_N со стороны остальных зарядов системы.

б) Каждое слагаемое суммы 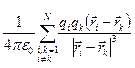представляет силу, действующую на i -ый

заряд со стороны k -го. Вся сумма б) равна результирующей силе действующей на всю систему зарядов и равна нулю, т.к. каждая пара зарядов взаимодействует друг с другом с силами, результирующая которых равна нулю.

1.3 В первоначально незаряженной системе в пространственно разделенных точках возникла пара зарядов q (см.рис.4). Выполняется ли при этом закон сохранения заряда:

 

Рис.4

а) если заряды возникли одновременно?

б) если заряды возникли в последовательные моменты времени?

Ответ:

а) Закон сохранения зарядов не выполняется, т.к. в малых областях, окружающих каждый заряд, произошло изменение заряда без переноса электричества через поверхность, ограничивающие эти области.

б) Закон сохранения заряда не выполняется, т.к. в период между возникновениями зарядов полный заряд замкнутой системы изменился без переноса электричества через поверхность, ограничивающую систему.

Дата добавления: 2015-08-10