Пример 1.8

Кольцо радиуса из тонкой проволоки имеет однородно распределенный заряд . Найдите модуль напряженности электрического поля на оси кольца как функцию расстояния до его центра. Исследуйте при .

Решение.

Разобьем заряд кольца на бесконечно малые элементы с зарядами , которые можно рассматривать как точечные. На оси кольца выберем произвольную точку с координатой . Заряд создаст в этой точке напряженность поля , направление которого показано на рисунке, а его величина равна:

.

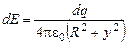Напряженность результирующего поля найдем, воспользовавшись принципом суперпозиции. В силу симметрии результирующее поле будет направлено вдоль оси (см. рисунок). Поэтому , где:

Учитывая, что , получим:

.

Суммируя вклады всех элементов кольца, найдем для проекции результирующего поля:

.

Рассмотрим напряженность поля на больших расстояниях .

,

т.е. на больших расстояниях система ведет себя как точечный заряд.

График представлен на рисунке.

Точки, в которых напряженность поля принимает максимальные значения, имеют координаты .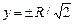

Дата добавления: 2015-08-10