II.Парабола

Параболою називають множину точок на площині, рівновіддалених від даної точки, яка називається фокусом і від даної прямої, яка називається директрисою.

Рівняння параболи з вершиною в початку координат, віссю симетрії якої є вісь Ох, має вигляд:

, (8.3)

де р – параметр параболи.

Якщо , то вітки параболи напрямлені вправо, якщо , то вітки напрямлені вліво (рис. 8.3).

Фокус параболи знаходиться у точці 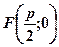. Рівняння директриси .

Рівняння параболи з вершиною в початку координат, віссю симетрії якої є вісь Оy, має вигляд:

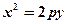. (8.4)

Якщо , то вітки направлені вгору, якщо , то вітки направлені вниз (рис. 8.4). Фокус такої параболи є точка , рівняння директриси .

Якщо вершина параболи – у точці 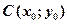, а вісь симетрії паралельна осі Оy, то рівняння має вигляд:

. (8.4*^')

Фокус цієї параболи 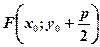, рівняння директриси .

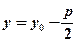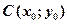Якщо вершина параболи знаходиться у точці , а вісь симетрії паралельна осі Ох, то рівняння параболи має вигляд:

. (8.3*^')

Фокус такої параболи , рівняння директриси .

Дата добавления: 2015-07-20